题目内容
【题目】在极坐标系中,曲线 ![]() 的极坐标方程分别为
的极坐标方程分别为 ![]() ,
, ![]() .
.
(1)求曲线 ![]() 和
和 ![]() 的公共点的个数;
的公共点的个数;
(2)过极点作动直线与曲线 ![]() 相交于点Q,在OQ上取一点P,使
相交于点Q,在OQ上取一点P,使 ![]()
![]() ,求点P的轨迹,并指出轨迹是什么图形.
,求点P的轨迹,并指出轨迹是什么图形.
【答案】
(1)解: ![]() 的直角坐标方程为
的直角坐标方程为 ![]() ,它表示圆心为
,它表示圆心为 ![]() ,半径为1的圆,
,半径为1的圆, ![]() 的直角坐标方程为
的直角坐标方程为 ![]() ,所以曲线
,所以曲线 ![]() 为直线,由于圆心到直线的距离为
为直线,由于圆心到直线的距离为 ![]() ,所以直线与圆相离,即曲线
,所以直线与圆相离,即曲线 ![]() 和
和 ![]() 的公共点个数为0
的公共点个数为0
(2)解:设 ![]() ,
, ![]() ,则
,则 ![]() 即
即 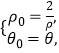 ①
①
因为点 ![]() 在曲线
在曲线 ![]() 上,所以
上,所以 ![]() ,②
,②
将①代入②,得 ![]() ,即
,即 ![]() ,此即为点P的轨迹方程,化为直角坐标方程为
,此即为点P的轨迹方程,化为直角坐标方程为 ![]() ,
,
因此,点P的轨迹是以 ![]() 为圆心,1为半径的圆
为圆心,1为半径的圆
【解析】1.根据ρ sin θ = y、ρ cos θ = x、.ρ2=x 2 + y 2化解出直角坐标方程;2.![]() 根据圆心到直线的距离与圆的半径比较确定直线与圆的位置关系即可得出答案;3.根据已知条件列出关系式,再根据C 2的极坐标方程确定点P的轨迹方程,最后根据P的极坐标方程转化为直角坐标方程确定轨迹图形。
根据圆心到直线的距离与圆的半径比较确定直线与圆的位置关系即可得出答案;3.根据已知条件列出关系式,再根据C 2的极坐标方程确定点P的轨迹方程,最后根据P的极坐标方程转化为直角坐标方程确定轨迹图形。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】通过随机调查询问110名性别不同的高中生是否爱好某项运动,得到如下的列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由 ![]() 计算得
计算得 ![]()
附表:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
C.有99%以上的把握认为“爱好该项运动与性别无关”
D.有99%以上的把握认为“爱好该项运动与性别有关”