题目内容
已知首项为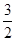 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
(1)求数列{an}的通项公式;
(2)设Tn=Sn-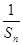 (n∈N*),求数列{Tn}的最大项的值与最小项的值.
(n∈N*),求数列{Tn}的最大项的值与最小项的值.
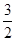 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.(1)求数列{an}的通项公式;
(2)设Tn=Sn-
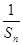 (n∈N*),求数列{Tn}的最大项的值与最小项的值.
(n∈N*),求数列{Tn}的最大项的值与最小项的值.(1)(-1)n-1 (2)
(2)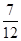
 (2)
(2)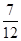
(1)解 设等比数列{an}的公比为q,因为S3+a3,S5+a5,S4+a4成等差数列,所以S5+a5-S3-a3=S4+a4-S5-a5,即4a5=a3,于是q2= =
=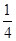 .
.
又{an}不是递减数列且a1=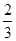 ,所以q=-
,所以q=- .
.
故等比数列{an}的通项公式为
an=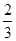 ×
×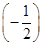 n-1=(-1)n-1
n-1=(-1)n-1 .
.
(2)由(1)得Sn=1-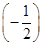 n=
n=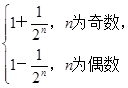 ,当n为奇数时,Sn随n的增大而减小,所以1<Sn≤S1=
,当n为奇数时,Sn随n的增大而减小,所以1<Sn≤S1=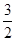 ,故0<Sn-
,故0<Sn-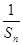 ≤S1-
≤S1-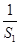 =
=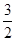 -
-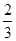 =
=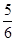
当n为偶数时,Sn随n的增大而增大,所以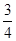 =S2≤Sn<1,故0>Sn-
=S2≤Sn<1,故0>Sn-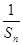 ≥S2-
≥S2-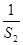 =
=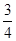 -
- =-
=-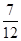 .
.
综上,对于n∈N*,总有-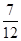 ≤Sn-
≤Sn-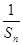 ≤
≤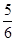 .
.
所以数列{Tn}最大项的值为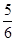 ,
,
最小项的值为-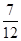 .
.
 =
=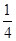 .
.又{an}不是递减数列且a1=
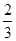 ,所以q=-
,所以q=- .
.故等比数列{an}的通项公式为
an=
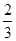 ×
×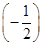 n-1=(-1)n-1
n-1=(-1)n-1 .
.(2)由(1)得Sn=1-
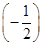 n=
n=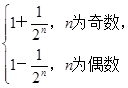 ,当n为奇数时,Sn随n的增大而减小,所以1<Sn≤S1=
,当n为奇数时,Sn随n的增大而减小,所以1<Sn≤S1=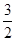 ,故0<Sn-
,故0<Sn-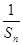 ≤S1-
≤S1-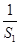 =
=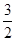 -
-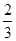 =
=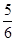
当n为偶数时,Sn随n的增大而增大,所以
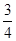 =S2≤Sn<1,故0>Sn-
=S2≤Sn<1,故0>Sn-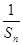 ≥S2-
≥S2-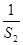 =
=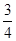 -
- =-
=-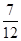 .
.综上,对于n∈N*,总有-
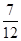 ≤Sn-
≤Sn-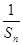 ≤
≤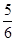 .
.所以数列{Tn}最大项的值为
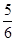 ,
,最小项的值为-
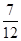 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
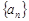 的前
的前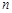 项和为
项和为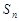 ,首项
,首项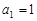 ,点
,点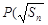 ,
,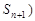 在曲线
在曲线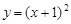 上.
上.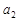 ,
,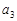 ;
;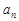 ;
;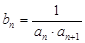 ,
,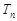 表示数列
表示数列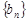 的前项和,若
的前项和,若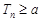 恒成立,求
恒成立,求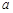 的取值范围.
的取值范围.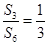 ,则
,则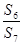 =________.
=________.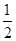
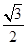
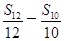 =2,则S2 014的值等于( ).
=2,则S2 014的值等于( ).