题目内容
设函数f(x)是定义在R上的偶函数,且f(x+2)=f(x)恒成立;当x∈[0,1]时,f(x)=x3-4x+3.有下列命题:
①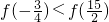 ;
;
②当x∈[-1,0]时f(x)=x3+4x+3;
③f(x)(x≥0)的图象与x轴的交点的横坐标由小到大构成一个无穷等差数列;
④关于x的方程f(x)=|x|在x∈[-3,4]上有7个不同的根.
其中真命题的个数为
- A.1个
- B.2个
- C.3个
- D.4个
B
分析:①因为函数f(x)是定义在R上的偶函数,所以 ;又因为对于任意的x等式f(x+2)=f(x)恒成立,所以
;又因为对于任意的x等式f(x+2)=f(x)恒成立,所以
f( )可化为f(
)可化为f( ),因为
),因为 都在[0,1]上,所以可以比较
都在[0,1]上,所以可以比较 大小,通过计算可得
大小,通过计算可得 .故可知①正确.
.故可知①正确.
②当x∈[-1,0]时,则-x∈[0,1],于是f(x)=f(-x)=(-x)3-4(-x)+3=-x3+4x+3≠x3+4x+3.故可知②不正确.
③因为f′(x)=3x2-4,所以当x∈[0,1]时,可知f(x)在x∈[0,1]上单调递减.又因为f(0)=3,f(1)=0,所以
f(x)=0在x∈[0,1]时只有一个根1;同时,因为f(x)是偶函数,所以f(x)在x∈[-1,0]上亦有且只有一个根-1,又因为对于任意的x等式f(x+2)=f(x)恒成立,所以有f(1)=f(3)=f(5)=…
故f(x)(x≥0)的图象与x轴的交点的横坐标为:1,3,5,….从而可判断出③正确.
④由③可知f(x)在x∈[0,1]上单调递减,且0≤f(x)≤3,则函数y=f(x)与y=|x|的图象在x∈[0,1]上有且只有有一个交点,即方程f(x)=|x|在x∈[0,1]上有且只有一个根,设为x1.由于函数f(x)是定义在R上的偶函数,所以f(-x1)=f(x1)=|-x1|,即-x1也是方程f(x)=|x|的一个根,这就是说:方程f(x)=|x|在x∈[-1,1]上有且只有两个根x1,-x1.同理,方程f(x)=|x|分别在x∈[1,2]、[2,3]上各有一个根,设为x2,x3;易知,方程f(x)=|x|分别在x∈[-2,-1]、[-3,-2]上亦各有一个根,且为-x2,-x3.在x∈(3,4]上,0<f(x)≤3,而3<|x|,故方程f(x)=|x|无根.综上可知:方程f(x)=|x|在x∈[-3,4]上共有6个根.因此④不正确.
解答:①∵函数f(x)是定义在R上的偶函数,∴ =
=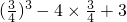 =
= ;
;
又∵对于任意的x等式f(x+2)=f(x)恒成立,
∴f( )=f(6+
)=f(6+ )=f(
)=f( )=f(2-
)=f(2- )=f(
)=f( )=f(
)=f( )=
)=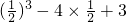 =
=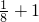 >f(
>f( ).
).
故可知①正确.
②当x∈[-1,0]时,则-x∈[0,1],于是f(x)=f(-x)=(-x)3-4(-x)+3=-x3+4x+3≠x3+4x+3.
故可知②不正确.
③因为f′(x)=3x2-4,所以当x∈[0,1]时,恒有f′(x)<0成立,故f(x)在x∈[0,1]时单调递减.
又因为f(0)=3,f(1)=0,所以f(x)=0在x∈[0,1]时有且只有一个根1;同理f(x)=0在x∈[-1,0]上有且只有一个根-1.
又因为对于任意的x等式f(x+2)=f(x)恒成立,所以有f(-1)=f(1)=f(3)=f(5)=…;
故f(x)(x≥0)的图象与x轴的交点的横坐标为:1,3,5,….是由小到大构成一个无穷等差数列{2n-1}.
故③正确.
④由③可知f(x)在x∈[0,1]时单调递减,且0≤f(x)≤3,
则函数y=f(x)与y=|x|的图象在x∈[0,1]上有且只有有一个交点,即方程f(x)=|x|在x∈[0,1]上有且只有一个根,设为x1.
由于函数f(x)是定义在R上的偶函数,所以f(-x1)=f(x1)=|-x1|,即-x1也是方程f(x)=|x|的一个根.
同理,方程f(x)=|x|分别在x∈[1,2]、[2,3]上各有一个根,设为x2,x3;易知,方程f(x)=|x|分别在x∈[-2,-1]、[-3,-2]上亦各有一个根,且为-x2,-x3.
在x∈(3,4]上,0<f(x)≤3,而3<|x|,故方程f(x)=|x|无根.
综上可知:方程f(x)=|x|在x∈[-3,4]上共有6个根.因此④不正确.
综上可知①、③正确.
点评:此题综合考查了函数的单调性、奇偶性、周期性及方程的根,等差数列等知识;还考查了数形结合的思想方法.
分析:①因为函数f(x)是定义在R上的偶函数,所以
 ;又因为对于任意的x等式f(x+2)=f(x)恒成立,所以
;又因为对于任意的x等式f(x+2)=f(x)恒成立,所以f(
 )可化为f(
)可化为f( ),因为
),因为 都在[0,1]上,所以可以比较
都在[0,1]上,所以可以比较 大小,通过计算可得
大小,通过计算可得 .故可知①正确.
.故可知①正确.②当x∈[-1,0]时,则-x∈[0,1],于是f(x)=f(-x)=(-x)3-4(-x)+3=-x3+4x+3≠x3+4x+3.故可知②不正确.
③因为f′(x)=3x2-4,所以当x∈[0,1]时,可知f(x)在x∈[0,1]上单调递减.又因为f(0)=3,f(1)=0,所以
f(x)=0在x∈[0,1]时只有一个根1;同时,因为f(x)是偶函数,所以f(x)在x∈[-1,0]上亦有且只有一个根-1,又因为对于任意的x等式f(x+2)=f(x)恒成立,所以有f(1)=f(3)=f(5)=…
故f(x)(x≥0)的图象与x轴的交点的横坐标为:1,3,5,….从而可判断出③正确.
④由③可知f(x)在x∈[0,1]上单调递减,且0≤f(x)≤3,则函数y=f(x)与y=|x|的图象在x∈[0,1]上有且只有有一个交点,即方程f(x)=|x|在x∈[0,1]上有且只有一个根,设为x1.由于函数f(x)是定义在R上的偶函数,所以f(-x1)=f(x1)=|-x1|,即-x1也是方程f(x)=|x|的一个根,这就是说:方程f(x)=|x|在x∈[-1,1]上有且只有两个根x1,-x1.同理,方程f(x)=|x|分别在x∈[1,2]、[2,3]上各有一个根,设为x2,x3;易知,方程f(x)=|x|分别在x∈[-2,-1]、[-3,-2]上亦各有一个根,且为-x2,-x3.在x∈(3,4]上,0<f(x)≤3,而3<|x|,故方程f(x)=|x|无根.综上可知:方程f(x)=|x|在x∈[-3,4]上共有6个根.因此④不正确.
解答:①∵函数f(x)是定义在R上的偶函数,∴
 =
=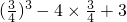 =
= ;
;又∵对于任意的x等式f(x+2)=f(x)恒成立,
∴f(
 )=f(6+
)=f(6+ )=f(
)=f( )=f(2-
)=f(2- )=f(
)=f( )=f(
)=f( )=
)=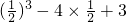 =
=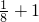 >f(
>f( ).
).故可知①正确.
②当x∈[-1,0]时,则-x∈[0,1],于是f(x)=f(-x)=(-x)3-4(-x)+3=-x3+4x+3≠x3+4x+3.
故可知②不正确.
③因为f′(x)=3x2-4,所以当x∈[0,1]时,恒有f′(x)<0成立,故f(x)在x∈[0,1]时单调递减.
又因为f(0)=3,f(1)=0,所以f(x)=0在x∈[0,1]时有且只有一个根1;同理f(x)=0在x∈[-1,0]上有且只有一个根-1.
又因为对于任意的x等式f(x+2)=f(x)恒成立,所以有f(-1)=f(1)=f(3)=f(5)=…;
故f(x)(x≥0)的图象与x轴的交点的横坐标为:1,3,5,….是由小到大构成一个无穷等差数列{2n-1}.
故③正确.
④由③可知f(x)在x∈[0,1]时单调递减,且0≤f(x)≤3,
则函数y=f(x)与y=|x|的图象在x∈[0,1]上有且只有有一个交点,即方程f(x)=|x|在x∈[0,1]上有且只有一个根,设为x1.
由于函数f(x)是定义在R上的偶函数,所以f(-x1)=f(x1)=|-x1|,即-x1也是方程f(x)=|x|的一个根.
同理,方程f(x)=|x|分别在x∈[1,2]、[2,3]上各有一个根,设为x2,x3;易知,方程f(x)=|x|分别在x∈[-2,-1]、[-3,-2]上亦各有一个根,且为-x2,-x3.
在x∈(3,4]上,0<f(x)≤3,而3<|x|,故方程f(x)=|x|无根.
综上可知:方程f(x)=|x|在x∈[-3,4]上共有6个根.因此④不正确.
综上可知①、③正确.
点评:此题综合考查了函数的单调性、奇偶性、周期性及方程的根,等差数列等知识;还考查了数形结合的思想方法.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目