题目内容
设函数f(x)是定义在R上的偶函数.若当x≥0时,f(x)=
(1)求f(x)在(-∞,0)上的解析式.
(2)请你作出函数f(x)的大致图象.
(3)当0<a<b时,若f(a)=f(b),求ab的取值范围.
(4)若关于x的方程f2(x)+bf(x)+c=0有7个不同实数解,求b,c满足的条件.
|
|
(1)求f(x)在(-∞,0)上的解析式.
(2)请你作出函数f(x)的大致图象.
(3)当0<a<b时,若f(a)=f(b),求ab的取值范围.
(4)若关于x的方程f2(x)+bf(x)+c=0有7个不同实数解,求b,c满足的条件.
分析:(1)设x∈(-∞,0)则-x∈(0,+∞),代入大于零的解析式,然后根据偶函数的性质即可求出f(x)在(-∞,0)上的解析式;
(2)利用分段函数的特点,分别在坐标系下画出函数的图象;
(3)因为0<a<b,所以f(a)=f(b)建立等式关系,然后利用基本不等式即可求出ab的范围;
(4)根据图象可知对于方程f(x)=a,当a=0时,方程有3个根;当0<a<1时,方程有4个根,当a≥1时,方程有2个根;当a<0时,方程无解,则要使关于x的方程f2(x)+bf(x)+c=0有7个不同实数解,关于f(x)的方程f2(x)+bf(x)+c=0有一个在区间(0,1)的正实数根和一个等于零的根,即可求出b、c满足的条件.
(2)利用分段函数的特点,分别在坐标系下画出函数的图象;
(3)因为0<a<b,所以f(a)=f(b)建立等式关系,然后利用基本不等式即可求出ab的范围;
(4)根据图象可知对于方程f(x)=a,当a=0时,方程有3个根;当0<a<1时,方程有4个根,当a≥1时,方程有2个根;当a<0时,方程无解,则要使关于x的方程f2(x)+bf(x)+c=0有7个不同实数解,关于f(x)的方程f2(x)+bf(x)+c=0有一个在区间(0,1)的正实数根和一个等于零的根,即可求出b、c满足的条件.
解答:解:(1)当x∈(-∞,0)时,f(x)=f(-x)=|1-
|=|1+
|.…(4分)
(2)f(x)的大致图象如下:.
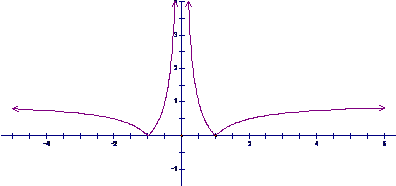 …(8分)
…(8分)
(3)因为0<a<b,所以f(a)=f(b)?|1-
|=|1-
|?(1-
)2=(1-
)2?
+
=2,…(11分)?a+b=2ab>2
解得ab的取值范围是(1,+∞).…(13分)
(4)由(2),对于方程f(x)=a,当a=0时,方程有3个根;当0<a<1时,方程有4个根,当a≥1时,方程有2个根;当a<0时,方程无解.…(15分)
所以,要使关于x的方程f2(x)+bf(x)+c=0有7个不同实数解,关于f(x)的方程f2(x)+bf(x)+c=0有一个在区间(0,1)的正实数根和一个等于零的根.
所以c=0,f(x)=-b∈(0,1),即-1<b<0,c=0.…(18分)
| 1 |
| -x |
| 1 |
| x |
(2)f(x)的大致图象如下:.
 …(8分)
…(8分)(3)因为0<a<b,所以f(a)=f(b)?|1-
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| ab |
解得ab的取值范围是(1,+∞).…(13分)
(4)由(2),对于方程f(x)=a,当a=0时,方程有3个根;当0<a<1时,方程有4个根,当a≥1时,方程有2个根;当a<0时,方程无解.…(15分)
所以,要使关于x的方程f2(x)+bf(x)+c=0有7个不同实数解,关于f(x)的方程f2(x)+bf(x)+c=0有一个在区间(0,1)的正实数根和一个等于零的根.
所以c=0,f(x)=-b∈(0,1),即-1<b<0,c=0.…(18分)
点评:本题主要考查了函数的奇偶性,以及函数解析式和函数图象,同时考查了根的存在性及根的个数判断,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目