题目内容
【题目】
已知函数![]() (
(![]() 是自然对数的底数).
是自然对数的底数).
(1)若曲线![]() 在
在![]() 处的切线也是抛物线
处的切线也是抛物线![]() 的切线,求
的切线,求![]() 的值;
的值;
(2)若对于任意![]() 恒成立,试确定实数
恒成立,试确定实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,是否存在
时,是否存在![]() ,使曲线
,使曲线![]() 在点
在点![]() 处的切线斜率与
处的切线斜率与![]() 在
在![]() 上的最小值相等?若存在,求符合条件的
上的最小值相等?若存在,求符合条件的![]() 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() (3)相等,一个.
(3)相等,一个.
【解析】
(1)求出![]() 在
在![]() 的切线,与
的切线,与![]() 联立,根据切线与抛物线只有一个交点,则
联立,根据切线与抛物线只有一个交点,则![]() ;(2)分
;(2)分![]() ,
,![]() ,
,![]() 根据导数讨论;(3)转化为函数的零点通过导数求解.
根据导数讨论;(3)转化为函数的零点通过导数求解.
(1)![]() ,
,
所以在![]() 处的切线为
处的切线为![]()
即:![]()
与![]() 联立,消去
联立,消去![]() 得
得![]() ,
,
由![]() 知,
知,![]() 或
或![]()
(2)![]()
①当![]() 时,
时,![]() 在
在![]() 上单调递增,且当
上单调递增,且当![]() 时,
时,![]() ,
,
![]() ,故
,故![]() 不恒成立,所以
不恒成立,所以![]() 不合题意 ;
不合题意 ;
②当![]() 时,
时,![]() 对
对![]() 恒成立,所以
恒成立,所以![]() 符合题意;
符合题意;
③当![]() 时令
时令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
故![]() 在
在![]() 上是单调递减,在
上是单调递减,在![]() 上是单调递增,
上是单调递增,
所以![]()
![]() 又
又![]() ,
,![]() ,
,
综上:![]()
(3)当![]() 时,
时,
由(2)知![]() ,
,
设![]() ,
,
则![]() ,
,
假设存在实数![]() ,使曲线
,使曲线![]() 在点
在点![]() 处的切线斜率与
处的切线斜率与![]() 在
在![]() 上的最小值相等,
上的最小值相等,![]() 即为方程的解,
即为方程的解,
令![]() 得:
得:![]() ,
,
因为![]() , 所以
, 所以![]() .
.
令![]() ,则
,则![]() ,
,
当![]() 是
是![]() ,当
,当![]() 时
时![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() ,故方程
,故方程![]() 有唯一解为1,
有唯一解为1,
所以存在符合条件的![]() ,且仅有一个
,且仅有一个![]() .
.

【题目】2020年春季,某出租汽车公司决定更换一批新的小汽车以代替原来报废的出租车,现有![]() 两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:
两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:
使用寿命年数 | 5年 | 6年 | 7年 | 8年 | 总计 |
| 10 | 20 | 45 | 25 | 100 |
| 15 | 35 | 40 | 10 | 100 |
(1)填写下表,并判断是否有![]() 的把握认为出租车的使用寿命年数与汽车车型有关?
的把握认为出租车的使用寿命年数与汽车车型有关?
使用寿命不高于 | 使用寿命不低于 | 总计 | |
| |||
| |||
总计 |
(2)司机师傅小李准备在一辆开了![]() 年的
年的![]() 型车和一辆开了
型车和一辆开了![]() 年的
年的![]() 型车中选择,为了尽最大可能实现
型车中选择,为了尽最大可能实现![]() 年内(含
年内(含![]() 年)不换车,试通过计算说明,他应如何选择.
年)不换车,试通过计算说明,他应如何选择.
附: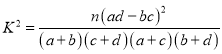 ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |