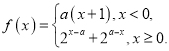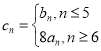题目内容
【题目】已知函数
.
（1）讨论函数
的单调区间；
（2）若函数的图象与
轴相切，求证：对于任意的
.
【答案】（1）答案不唯一，具体见解析（2）证明见解析；
【解析】
（1）先对函数进行求导，然后根据实数
的取值情况进行讨论，结合导数的正负，判断求解函数的单调性与单调区间；
（2）因为函数
的图象与
轴相切，由（1）可知，
且
，可求出，当
时，
恒成立，为证明对于任意的
成立，只要证明
即可，令
，然后在利用导数在函数最值中的应用，即可证明
，由此即可证明不等式成立.
解：（1）函数的定义域是
，
当
时，
，
在
上单调递减；
当时，
，
在
上单调递减；
，
在
上单调递增.
（2）证明：因为函数的图象与轴相切，设切点为
，
，解得
，
，
又当时，恒成立，
令
，
由
，得
，
是
的最大值，
，
成立.
【题目】随着网上购物的普及，传统的实体店遭受到了强烈的冲击，某商场实体店近九年来的纯利润如下表所示：
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
时间代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
实体店纯利润 | 2 | 2.3 | 2.5 | 2.9 | 3 | 2.5 | 2.1 | 1.7 | 1.2 |
根据这9年的数据，对
和
作线性相关性检验，求得样本相关系数的绝对值为0.254；根据后5年的数据，对
和作线性相关性检验，求得样本相关系数的绝对值为0.985；
（1）如果要用线性回归方程预测该商场2019年实体店纯利润，现有两个方案：
方案一：选取这9年的数据，进行预测；
方案二：选取后5年的数据进行预测.
从生活实际背景以及相关性检验的角度分析，你觉得哪个方案更合适.
附：相关性检验的临界值表：
| 小概率 | |
0.05 | 0.01 | |
3 | 0.878 | 0.959 |
7 | 0.666 | 0.798 |
（2）某机构调研了大量已经开店的店主，据统计，只开网店的占调查总人数的
，既开网店又开实体店的占调查总人数的
，现以此调查统计结果作为概率，若从上述统计的店主中随机抽查了5位，求只开实体店的人数的分布列及期望.
【题目】在传染病学中，通常把从致病刺激物侵人机体或者对机体发生作用起，到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期. 一研究团队统计了某地区1000名患者的相关信息，得到如下表格：
潜伏期（单位：天） |
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
（1）求这1000名患者的潜伏期的样本平均数x (同一组中的数据用该组区间的中点值作代表) ；
（2）该传染病的潜伏期受诸多因素的影响，为研究潜伏期与患者年龄的关系，以潜伏期是否超过6天为标准进行分层抽样，从上述1000名患者中抽取200人，得到如下列联表
潜伏期 | 潜伏期 | 总计 | |
|
| ||
|
| ||
总计 |
|
（3）以这1000名患者的潜伏期超过6天的频率，代替该地区1名患者潜伏期超过6天发生的概率，每名患者的潜伏期是否超过6天相互独立，为了深入研究，该研究团队随机调查了20名患者，其中潜伏期超过6天的人数最有可能（即概率最大）是多少？
附：
|
|
|
|
|
|
|
|
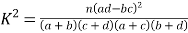，其中
.
