题目内容
(本小题满分14分)
已知椭圆G与双曲线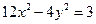 有相同的焦点,且过点
有相同的焦点,且过点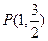 .
.
(1)求椭圆G的方程;
(2)设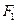 、
、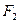 是椭圆G的左焦点和右焦点,过
是椭圆G的左焦点和右焦点,过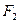 的直线
的直线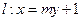 与椭圆G相交于A、B两点,请问
与椭圆G相交于A、B两点,请问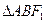 的内切圆M的面积是否存在最大值?若存在,求出这个最大值及直线
的内切圆M的面积是否存在最大值?若存在,求出这个最大值及直线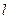 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
已知椭圆G与双曲线
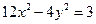 有相同的焦点,且过点
有相同的焦点,且过点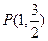 .
.(1)求椭圆G的方程;

(2)设
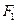 、
、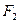 是椭圆G的左焦点和右焦点,过
是椭圆G的左焦点和右焦点,过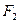 的直线
的直线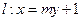 与椭圆G相交于A、B两点,请问
与椭圆G相交于A、B两点,请问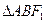 的内切圆M的面积是否存在最大值?若存在,求出这个最大值及直线
的内切圆M的面积是否存在最大值?若存在,求出这个最大值及直线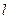 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.解:(1)双曲线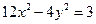 的焦点坐标为
的焦点坐标为 ,所以椭圆的焦点坐标为
,所以椭圆的焦点坐标为 ………………1分
………………1分
设椭圆的长轴长为 ,则
,则 ,即
,即 ,
,
又 ,所以
,所以 ∴椭圆
∴椭圆 G的方程
G的方程 ………………5分
………………5分
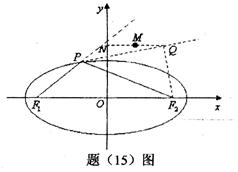
(2)如图,设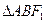 内切圆M的半径为
内切圆M的半径为 ,与直线
,与直线 的切点为C,则三角形
的切点为C,则三角形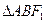 的面积等于
的面积等于 的面积+
的面积+ 的面积+
的面积+ 的面积.
的面积.
即

当 最大时,
最大时, 也最大,
也最大, 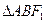 内切圆的面积也最大, ………………7分
内切圆的面积也最大, ………………7分
设 、
、 (
( ),则
),则 ,
,
由 ,得
,得 ,………………9分
,………………9分
解得 ,
, ,
,
∴ ,令
,令 ,则
,则 ,且
,且 ,
,
有 ,令
,令 ,则
,则 ,……………11分
,……………11分
当 时,
时, ,
, 在
在 上单调递增,有
上单调递增,有 ,
, ,
,
即当 ,
, 时,
时, 有最大值
有最大值 ,得
,得 ,这时所求内切圆的面积为
,这时所求内切圆的面积为 ,……………12分
,……………12分
∴存在直线 ,
,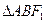 的内切圆M的面积最大值为
的内切圆M的面积最大值为 . ………………13分
. ………………13分
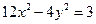 的焦点坐标为
的焦点坐标为 ,所以椭圆的焦点坐标为
,所以椭圆的焦点坐标为 ………………1分
………………1分设椭圆的长轴长为
 ,则
,则 ,即
,即 ,
,又
 ,所以
,所以 ∴椭圆
∴椭圆 G的方程
G的方程 ………………5分
………………5分(2)如图,设
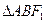 内切圆M的半径为
内切圆M的半径为 ,与直线
,与直线 的切点为C,则三角形
的切点为C,则三角形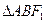 的面积等于
的面积等于 的面积+
的面积+ 的面积+
的面积+ 的面积.
的面积.即


当
 最大时,
最大时, 也最大,
也最大, 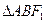 内切圆的面积也最大, ………………7分
内切圆的面积也最大, ………………7分设
 、
、 (
( ),则
),则 ,
,由
 ,得
,得 ,………………9分
,………………9分解得
 ,
, ,
,∴
 ,令
,令 ,则
,则 ,且
,且 ,
,有
 ,令
,令 ,则
,则 ,……………11分
,……………11分当
 时,
时, ,
, 在
在 上单调递增,有
上单调递增,有 ,
, ,
,即当
 ,
, 时,
时, 有最大值
有最大值 ,得
,得 ,这时所求内切圆的面积为
,这时所求内切圆的面积为 ,……………12分
,……………12分∴存在直线
 ,
,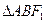 的内切圆M的面积最大值为
的内切圆M的面积最大值为 . ………………13分
. ………………13分略

练习册系列答案
相关题目
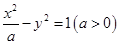 的离心率为
的离心率为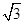 ,则
,则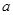 的值是
的值是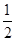
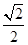
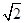
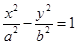 (a>0,b>0)的两个焦点为
(a>0,b>0)的两个焦点为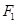 、
、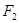 ,点A在双曲线
,点A在双曲线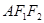 的面积为1,且
的面积为1,且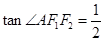 ,
,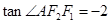 ,则
,则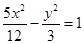

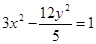
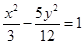
 与直线
与直线 相切于点A(1,1)。
相切于点A(1,1)。 的解析式;
的解析式; ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。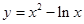 上任意一点,则点P到直线
上任意一点,则点P到直线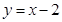 的最小距离为 ( )
的最小距离为 ( )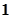
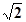
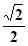
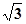
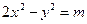 的一个焦点是
的一个焦点是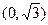 ,则
,则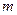 的值是__________.
的值是__________.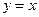 与抛物线C相交
与抛物线C相交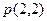 是AB的中点,则抛物线C的方程为_______________.
是AB的中点,则抛物线C的方程为_______________. 中,曲线
中,曲线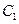 的参数方程为
的参数方程为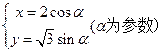 .在极坐标系(与直角坐标系
.在极坐标系(与直角坐标系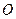 为极点,以
为极点,以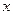 轴正半轴为极轴)中,曲线
轴正半轴为极轴)中,曲线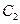 的方程为
的方程为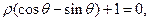 则
则
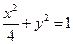 的焦点为
的焦点为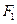 、
、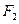 ,点
,点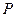 为椭圆上任意一点,过
为椭圆上任意一点,过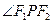 的外角平分线的垂线,垂足为点
的外角平分线的垂线,垂足为点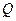 ,过点
,过点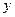 轴的垂线,垂足为
轴的垂线,垂足为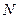 ,线段
,线段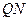 的中点为
的中点为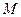 ,则点
,则点