题目内容
19．由曲线y=$\frac{1}{x}$，x=1，x=2，y=0所围成的封闭图形的面积为（ ）| A． | 4 | B． | 2 | C． | 2ln2 | D． | ln2 |
分析 首先利用定积分表示面积，然后计算即可．
解答 解：由曲线y=$\frac{1}{x}$，x=1，x=2，y=0所围成的封闭图形的面积为：${∫}_{1}^{2}\frac{1}{x}dx$=lnx|${\;}_{1}^{2}$=ln2；
故选D．
点评 本题考查了运用定积分求瞿塘峡的面积；关键是正确利用定积分表示面积，然后正确计算．
练习册系列答案
相关题目
9．过曲线C：y=$\frac{1}{x}$（x＞0）上一点P（x0，y0）作曲线C的切线，若切线的斜率为-4，则x0等于（ ）
| A． | 2 | B． | $\frac{1}{2}$ | C． | 4 | D． | $\frac{1}{4}$ |
10．设$\overrightarrow{e_1}，\overrightarrow{e_2}$为两不共线的向量，则$\overrightarrow a=\overrightarrow{e_1}+λ\overrightarrow{e_2}$与$\overrightarrow b=-（{2\overrightarrow{e_2}-3\overrightarrow{e_1}}）$共线的条件是（ ）
| A． | λ=$\frac{3}{2}$ | B． | λ=$\frac{2}{3}$ | C． | λ=-$\frac{2}{3}$ | D． | λ=-$\frac{3}{2}$ |
7．下列幂函数中，过点（0，0），（1，1）的偶函数是（ ）
| A． | y=x${\;}^{\frac{1}{2}}$ | B． | y=x${\;}^{\frac{1}{3}}$ | C． | y=x-2 | D． | y=x4 |
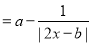是偶函数，
为实常数．
的值；
时，是否存在
，使得函数
在区间
上的函数值组成的集合也是
，若存在，求出
，
的值；否则，说明理由．
，则
的真子集可以是（ ）
B．
C．
D．