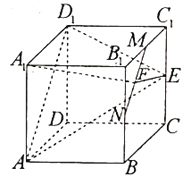
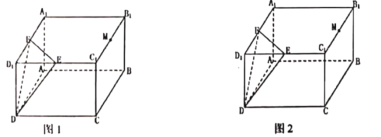
题目内容
【题目】已知动点![]() 到定点
到定点![]() 的距离之和为4.
的距离之和为4.
(1)求动点![]() 的轨迹方程
的轨迹方程![]()
(2)若轨迹![]() 与直线
与直线![]() 交于
交于![]() 两点,且
两点,且![]() 求
求![]() 的值.
的值.
(3)若点![]() 与点
与点![]() 在轨迹
在轨迹![]() 上,且点
上,且点![]() 在第一象限,点
在第一象限,点![]() 在第二象限,点
在第二象限,点![]() 与点
与点![]() 关于原点对称,求证:当
关于原点对称,求证:当![]() 时,三角形
时,三角形![]() 的面积为定值.
的面积为定值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)定值
;(3)定值![]() ,见解析
,见解析
【解析】
(1)求得椭圆的![]() ,即可求动点
,即可求动点![]() 的轨迹方程
的轨迹方程![]()
(2)将直线![]() 代入椭圆方程
代入椭圆方程![]() ,可得
,可得![]() 的方程,运用韦达定理和判别式大于0,由弦长公式,解方程即可得到所求值;
的方程,运用韦达定理和判别式大于0,由弦长公式,解方程即可得到所求值;
(3)求出直线AB的方程,运用点到直线的距离公式求得P到直线AB的距离,弦长AB,运用三角形的面积公式可得![]() ,再由A,P满足椭圆方程,结合条件
,再由A,P满足椭圆方程,结合条件![]() ,计算即可得到三角形
,计算即可得到三角形![]() 的面积为定值.
的面积为定值.
(1)动点Q到两定点![]() 、
、![]() 的距离和为4,满足椭圆的定义,且
的距离和为4,满足椭圆的定义,且![]()
![]()
![]() ,
,![]() 动点
动点![]() 的轨迹方程
的轨迹方程![]() :
:![]()
(2)将直线![]() 代入椭圆方程
代入椭圆方程![]() ,可得
,可得![]() ,
,![]() ,解得
,解得![]() ,
,
设![]()
![]()
则![]()
![]()
即有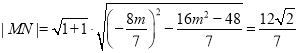 ,
,
解得![]() ,满足
,满足![]()
(3)证明:直线AB的方程为![]() ,即为
,即为![]() ,
,
可得![]() 到直线AB的距离为
到直线AB的距离为 ,
,![]() ,
,
则![]() ═
═![]() ,
,
由![]() ,得
,得![]()
![]() 因为
因为![]()
![]()
可得![]()
![]()
则![]()
由![]() ,可得
,可得![]()
![]()
即有![]()
故当![]() 时,三角形
时,三角形![]() 的面积为定值
的面积为定值![]()

练习册系列答案
相关题目
【题目】目前有声书正受着越来越多人的喜爱.某有声书公司为了解用户使用情况,随机选取了![]() 名用户,统计出年龄分布和用户付费金额(金额为整数)情况如下图.
名用户,统计出年龄分布和用户付费金额(金额为整数)情况如下图.
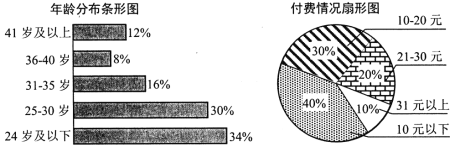
有声书公司将付费高于![]() 元的用户定义为“爱付费用户”,将年龄在
元的用户定义为“爱付费用户”,将年龄在![]() 岁及以下的用户定义为“年轻用户”.已知抽取的样本中有
岁及以下的用户定义为“年轻用户”.已知抽取的样本中有![]() 的“年轻用户”是“爱付费用户”.
的“年轻用户”是“爱付费用户”.
(1)完成下面的![]() 列联表,并据此资料,能否有
列联表,并据此资料,能否有![]() 的把握认为用户“爱付费”与其为“年轻用户”有关?
的把握认为用户“爱付费”与其为“年轻用户”有关?
爱付费用户 | 不爱付费用户 | 合计 | |
年轻用户 | |||
非年轻用户 | |||
合计 |
(2)若公司采用分层抽样方法从“爱付费用户”中随机选取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人进行访谈,求抽取的
人进行访谈,求抽取的![]() 人恰好都是“年轻用户”的概率.
人恰好都是“年轻用户”的概率.
|
|
|
|
|
|
|
|
|
|
|
|
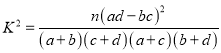 .
.