题目内容
9.某中学高三(1)班的一次数学单元测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.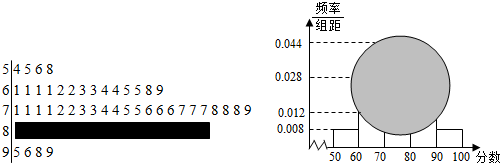
(1)求全班人数;
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间矩形的高;
(3)若要从分数在[80,100)之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在[90,100)之间的概率.
分析 (1)根据条件所给的茎叶图看出分数在[50,60)之间的频数,由频率分布直方图看出分数在[50,60)之间的频率,根据频率、频数和样本容量之间的关系解出样本容量.
(2)算出分数在[80,90)之间的人数,算出分数在[80,90)之间的频率,根据小矩形的面积是这一段数据的频率,做出矩形的高.
(3)由题意知本题是一个古典概型,试验包含的所有事件可以通过列举得到结果数,看出满足条件的事件数,根据古典概型公式和对立事件概率计算公式能得到结果
解答 解:(1)由茎叶图知:分数在[50,60)之间的频数为4.
由频率分布直方图知:分数在[50,60)之间的频率为0.008×10=0.08.
∴全班人数为$\frac{4}{0.08}$=50人.
(2)∵分数在[80,90)之间的人数为50-4-14-22-4=6人
∴分数在[80,90)之间的频率为$\frac{6}{50}$=0.12,
∴频率分布直方图中[80,90)间的矩形的高为$\frac{0.12}{10}$=0.012.
(3)∵分数在[80,90)间的人数为6,[90,100)间的人数为4,
∴要从分数在[80,100)之间的试卷中任取两份,基本事件总数n=${C}_{10}^{2}$=45,
两份试卷都在[80,90)之间的基本事件m=${C}_{6}^{2}$=15,
∴在抽取的试卷中,至少有一份分数在[90,100)之间的概率:
p=1-$\frac{m}{n}$=1-$\frac{15}{45}$=$\frac{2}{3}$.
点评 这是一个统计综合题,频数、频率和样本容量三者之间的关系是知二求一,这种问题会出现在选择和填空中,有的省份也会以大题的形式出现,把它融于统计问题中.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
4.已知函数f(x)=xa(0<a<1),下列说法中错误的是( )
| A. | 若x>1,则f(x)>1 | B. | 若0<x<1,则0<f(x)<1 | ||
| C. | 若f(x1)>f(x2),则x1>x2 | D. | 若0<x1<x2,则f(x1)>f(x2) |
14.已知函数f(x)=$\left\{\begin{array}{l}{-x+3a,x<0}\\{lo{g}_{a}(x+1),x≥0}\end{array}\right.$(a>0且a≠1)是R上的减函数,则a的取范围是( )
| A. | (0,1) | B. | [$\frac{1}{3},1$) | C. | (0,$\frac{1}{3}$] | D. | ($\frac{1}{3}$,1) |
18.函数f(x),g(x)均为奇函数,定义域都为[-a,a](a>0),则f(g(x))为( )
| A. | 奇函数 | B. | 偶函数 | C. | 非奇非偶函数 | D. | 无法判断奇偶性 |