题目内容
1. 如图在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{2}$,设E、F分别为PC、BD的中点.
如图在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{2}$,设E、F分别为PC、BD的中点.(1)求证:EF∥平面PAD;
(2)求证:平面PAB⊥平面PCD;
(3)求四棱锥P-ABCD的体积.
分析 (1)连接AC,则F是AC的中点,E为PC 的中点,证明EF∥PA,留言在线与平面平行的判定定理证明EF∥平面PAD;
(2)先证明CD⊥PA,然后证明PA⊥PD.利用直线与平面垂直的判定定理证明PA⊥平面PCD,最后根据面面垂直的判定定理即可得到面PAB⊥面PDC.
(3)利用面面垂直的性质,证明CD⊥平面PAD,计算P-ADC的体积,再计算求四棱锥P-ABCD的体积VP-ABCD.
解答 (1)证明:连接AC,由正方形性质可知,AC与BD相交于BD的中点F,F也为AC中点,E为PC中点.
所以在△CPA中,EF∥PA,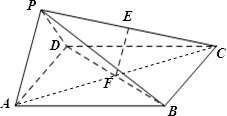
又PA?平面PAD,EF?平面PAD,
所以EF∥平面PAD;
(2)证明:平面PAD⊥平面ABCD
平面PAD∩面ABCD=AD⇒CD⊥平面PAD⇒CD⊥PA
正方形ABCD中CD⊥ADPA?平面PADCD?平面ABCD
又PA=PD=$\sqrt{2}$,AD=2,所以PA2+PD2=AD2
所以△PAD是等腰直角三角形,且∠APD=$\frac{π}{2}$,即PA⊥PD.
因为CD∩PD=D,且CD、PD?面PDC
所以PA⊥面PDC
又PA?面PAB,
所以面PAB⊥面PDC.
(3)解:因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
又CD⊥AD,所以CD⊥平面PAD,CD=2,
因为S△PAD=$\frac{1}{2}×(\sqrt{2})^{2}$=1
所以VP-ADC=VC-PAD=$\frac{1}{3}×1×2$=$\frac{2}{3}$,
所以VP-ABCD=2VP-ADC=$\frac{4}{3}$.
点评 本题考查直线与平面垂直的判定,直线与平面平行的判定的应用,考查体积的计算,考查逻辑推理能力.

练习册系列答案
相关题目
12.在△ABC中,$\overrightarrow{A{B}^{\;}}$2=$\overrightarrow{BA}$•$\overrightarrow{BC}$,$\overrightarrow{OA}$+$\overrightarrow{OC}$+$\overrightarrow{AB}$=0,且|$\overrightarrow{OA}$|=|$\overrightarrow{AB}$|=1,则$\overrightarrow{CA}$•$\overrightarrow{CB}$等于( )
| A. | 3 | B. | $\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | 2$\sqrt{3}$ |
16.设函数f(x)=|x-a|+|x-2|,若函数g(x)=(x+a)•f(x)的图象中心对称,则a的值为( )
| A. | 1 | B. | -2 | C. | 0 | D. | -$\frac{2}{3}$ |
10.已知等比数列{an}的各项均为正数,且公比q≠1,若a4、a5、2a3成等差数列,则公比q=( )
| A. | $\frac{1+\sqrt{3}}{2}$或$\frac{1-\sqrt{3}}{2}$ | B. | $\frac{1+\sqrt{17}}{4}$ | C. | $\frac{1+\sqrt{5}}{2}$或$\frac{1-\sqrt{5}}{2}$ | D. | $\frac{1+\sqrt{5}}{2}$ |
11.在半径为10cm的球面上有A,B,C三点,如果AB=8$\sqrt{3}$,∠ACB=60°,则球心O到平面ABC的距离为( )
| A. | 2cm | B. | 4cm | C. | 6cm | D. | 8cm |
 如图,边长为2的正方形ABCD中,点E,F分别在线段AB与BC上,且满足:BE=BF=$\frac{1}{2}$BC,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点P,并连结PB.
如图,边长为2的正方形ABCD中,点E,F分别在线段AB与BC上,且满足:BE=BF=$\frac{1}{2}$BC,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点P,并连结PB.