题目内容
 选修4-1:几何证明选讲
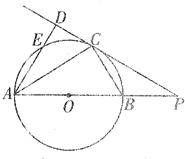
选修4-1:几何证明选讲如图,以AB为直径的⊙O上有一点C,过点C作⊙O的切线与AB延长线交于点P,AD⊥PC交PC的延长线于D,AD与⊙O相交于点E.
(1)求证:PB:PC=DC:AD;
(2)若AB=6,BC=3,求AE的长.
分析:(1)先根据PC与圆O相切于C点证得△APC∽△CPB,推出PB:PC=BC:AC;再结合∠ACB=90°以及AD⊥PC于D得到Rt△ACD∽Rt△ABC,进而得DC:AD=BC:AC,联立即可证明结论.
(2)先在△ABC中求出AC,再根据△ACD∽△ABC求出DC以及AD,再结合切割线定理即可求出结论.
(2)先在△ABC中求出AC,再根据△ACD∽△ABC求出DC以及AD,再结合切割线定理即可求出结论.
解答:(1)证明:
∵PC与圆O相切于C点,
∴∠CAB=∠PCB
∴△APC∽△CPB.
∴PB:PC=BC:AC.
又∵∠ACB=90°,
∴∠PCB+∠DCA=90°,
∵AD⊥PC于D
∴∠DAC+∠DCA=90°,
∴∠DAC=∠CAB.
∴Rt△ACD∽Rt△ABC,
∴DC:AD=BC:AC.
∴PB:PC=DC:AD.
(2)解:在△ABC中,AB=6,BC=3,
∴AC=3
.
由△ACD∽△ABC,以及AD⊥PC于D
∴DC=
,AD=
.
又由切割线定理得:DC2=AD•DE.
即
=
×(
-AE)
∴AE=3.
∵PC与圆O相切于C点,
∴∠CAB=∠PCB
∴△APC∽△CPB.
∴PB:PC=BC:AC.
又∵∠ACB=90°,
∴∠PCB+∠DCA=90°,
∵AD⊥PC于D
∴∠DAC+∠DCA=90°,
∴∠DAC=∠CAB.
∴Rt△ACD∽Rt△ABC,
∴DC:AD=BC:AC.
∴PB:PC=DC:AD.
(2)解:在△ABC中,AB=6,BC=3,
∴AC=3
| 3 |
由△ACD∽△ABC,以及AD⊥PC于D
∴DC=
3
| ||
| 2 |
| 9 |
| 2 |
又由切割线定理得:DC2=AD•DE.
即
| 27 |
| 4 |
| 9 |
| 2 |
| 9 |
| 2 |
∴AE=3.
点评:本题主要考查与圆有关的比例线段、相似三角形的判定及切线性质的应用.是对基础知识的综合考查.

练习册系列答案
相关题目
 选修4-1:几何证明选讲
选修4-1:几何证明选讲 A、选修4-1:几何证明选讲
A、选修4-1:几何证明选讲  选修4-1:几何证明选讲
选修4-1:几何证明选讲 (2012•徐州模拟)选修4-1:几何证明选讲
(2012•徐州模拟)选修4-1:几何证明选讲 (2013•南京二模)选修4-1:几何证明选讲
(2013•南京二模)选修4-1:几何证明选讲