题目内容
(本小题满分14分)已知椭圆![]() 的中心为原点,点
的中心为原点,点![]()
![]() 是它的一个焦点,直线
是它的一个焦点,直线![]() 过点
过点![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且当直线
两点,且当直线![]() 垂直于
垂直于![]() 轴时,
轴时,![]() .(Ⅰ)求椭圆
.(Ⅰ)求椭圆![]() 的方程;(Ⅱ)是否存在直线
的方程;(Ⅱ)是否存在直线![]() ,使得在椭圆
,使得在椭圆![]() 的右准线上可以找到一点
的右准线上可以找到一点![]() ,满足
,满足![]() 为正三角形.如果存在,求出直线
为正三角形.如果存在,求出直线![]() 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.
解:(Ⅰ)设椭圆![]() 的方程为:
的方程为:![]() ,则
,则![]() .…①1分
.…①1分
![]() 当
当![]() 垂直于
垂直于![]() 轴时,
轴时,![]() 两点坐标分别是
两点坐标分别是![]() 和
和![]() ,
,
![]() ,则
,则![]() ,即
,即![]() .……② …3分
.……② …3分
由①,②消去![]() ,得
,得![]() .
.
![]() 或
或![]() (舍去).
(舍去).
当![]() 时,
时,![]() .
.
因此,椭圆![]() 的方程为
的方程为![]() . …………………………5分
. …………………………5分
(Ⅱ)设存在满足条件的直线![]() .
.
(1)当直线![]() 垂直于
垂直于![]() 轴时,由(Ⅰ)的解答可知
轴时,由(Ⅰ)的解答可知![]() ,焦点
,焦点![]() 到右准线的距离为
到右准线的距离为![]() ,此时不满足
,此时不满足![]() .
.
因此,当直线![]() 垂直于
垂直于![]() 轴时不满足条件. …………………………7分
轴时不满足条件. …………………………7分
(2)当直线![]() 不垂直于
不垂直于![]() 轴时,设直线
轴时,设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .
.
由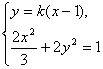
![]()
![]() ,
,
设![]() 两点的坐标分别为
两点的坐标分别为![]() 和
和![]() ,则
,则
![]() ,
,![]() .
.
![]()
![]()
![]() . …………………9分
. …………………9分
又设![]() 的中点为
的中点为![]() ,则
,则![]()
![]() .
.
当![]() 为正三角形时,直线
为正三角形时,直线![]() 的斜率为
的斜率为![]() .
.
![]() ,
,
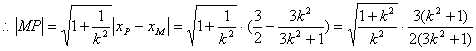 .
.
……
当![]() 为正三角形时,
为正三角形时,![]() ,即
,即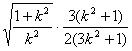 =
=![]() ,
,
解得![]() ,
,![]() . ……………………13分
. ……………………13分
因此,满足条件的直线![]() 存在,且直线
存在,且直线![]() 的方程为
的方程为![]() 或
或![]() .…14分
.…14分

练习册系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)