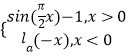Question

【题目】设p：关于x的不等式ax＞1的解集是{x|x＜0}；q：函数 的定义域为R．若p∨q是真命题，p∧q是假命题，求实数a的取值范围．

Answer 1

【答案】解：∵关于x的不等式ax＞1的解集是{x|x＜0}，∴0＜a＜1；故命题p为真时，0＜a＜1；
∵函数 的定义域为R，
∴ a≥ ，
由复合命题真值表知：若p∨q是真命题，p∧q是假命题，则命题p、q一真一假，
当p真q假时，则 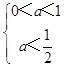0＜a＜ ；
当q真p假时，则 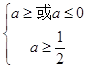a≥1，
综上实数a的取值范围是（0， ）∪[1，+∞）
【解析】根据指数函数的单调性求得命题p为真时a的取值范围；利用 求出命题q为真时a的范围，由复合命题真值表知：若p∨q是真命题，p∧q是假命题，则命题p、q一真一假，
分p真q假和q真p假两种情况求出a的范围，再求并集．
【考点精析】利用复合命题的真假对题目进行判断即可得到答案，需要熟知“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反；“p且q”形式复合命题当P与q同为真时为真，其他情况时为假；“p或q”形式复合命题当p与q同为假时为假，其他情况时为真．