题目内容
【题目】在直角坐标系中，已知圆C的圆心坐标为（2，0），半径为 
，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．，直线l的参数方程为： 
（t为参数）．
（1）求圆C和直线l的极坐标方程；
（2）点P的极坐标为（1， 
），直线l与圆C相交于A，B，求|PA|+|PB|的值．
【答案】
（1）解：圆C的直角坐标方程为（x﹣2）2+y2=2，
代入圆C得：（ρcosθ﹣2）2+ρ2sin2θ=2
化简得圆C的极坐标方程：ρ2﹣4ρcosθ+2=0
由 
得x+y=1，∴l的极坐标方程为ρcosθ+ρsinθ=1
（2）解：由 
得点P的直角坐标为P（0，1），
∴直线l的参数的标准方程可写成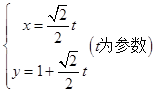 
代入圆C得： 
化简得： 
，
∴ 
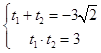，∴t1＜0，t2＜0
∴ 
【解析】（1） 代入圆C得圆C的极坐标方程；直线l的参数方程转化成普通方程，进而求得直线l的极坐标方程；（2）将直线l的参数方程代入圆的方程，求得关于t的一元二次方程，令A，B对应参数分别为t1 ， t2 ， 根据韦达定理、直线与圆的位置关系，即可求得|PA|+|PB|的值．
【题目】某商场销售某种品牌的空调器，每周周初购进一定数量的空调器，商场每销售一台空调器可获利500元，若供大于求，则每台多余的空调器需交保管费100元；若供不应求，则可从其他商店调剂供应，此时每台空调器仅获利润200元．
（Ⅰ）若该商场周初购进20台空调器，求当周的利润（单位：元）关于当周需求量n（单位：台，n∈N）的函数解析式f（n）；
（Ⅱ）该商场记录了去年夏天（共10周）空调器需求量n（单位：台），整理得表：
周需求量n | 18 | 19 | 20 | 21 | 22 |
频数 | 1 | 2 | 3 | 3 | 1 |
以10周记录的各需求量的频率作为各需求量发生的概率，若商场周初购进20台空调器，X表示当周的利润（单位：元），求X的分布列及数学期望．
