题目内容
13. 已知:过抛物线x2=4y的焦点F的直线交抛物线于A,B两个不同的点,过A,B分别作抛物线的切线,且二者相交于点C.
已知:过抛物线x2=4y的焦点F的直线交抛物线于A,B两个不同的点,过A,B分别作抛物线的切线,且二者相交于点C.(1)求证:$\overrightarrow{AB}$•$\overrightarrow{CF}$=0;
(2)求△ABC的面积的最小值.
分析 (1)设A(x1,y1),B(x2,y2),C(x0,y0).设AB:y=kx+1,代入抛物线方程得x2-4kx-4=0,由y=$\frac{1}{4}{x}^{2}$,可得y′=$\frac{1}{2}x$,分别得出直线AC,BC的方程联立解得x0=2k,y0=-1.对k分类讨论,k≠0时,可得kAB•kCF=-1,可得$\overrightarrow{AB}$•$\overrightarrow{CF}$=0;若k=0,即可得出$\overrightarrow{AB}$•$\overrightarrow{CF}$=0;
(2)由(1)知,点C到AB的距离d=|CF|=2$\sqrt{1+{k}^{2}}$,利用抛物线定义可得:|AB|=|AF|+|FB|=y1+y2+2,可得$S=\frac{1}{2}|AB|•d$.
解答 (1)证明:设A(x1,y1),B(x2,y2),C(x0,y0).
设直线AB方程:y=kx+1,代入x2=4y得x2-4kx-4=0,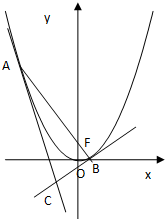
∴x1+x2=4k,x1x2=-4.
$y=\frac{1}{4}{x}^{2}$,y′=$\frac{1}{2}x$,
直线AC的方程为:$y-\frac{1}{4}{x}_{1}^{2}=\frac{1}{2}{x}_{1}(x-{x}_{1})$,直线BC的方程为:$y-\frac{1}{4}{x}_{2}^{2}=\frac{1}{2}{x}_{2}(x-{x}_{2})$,
联立解得x0=2k,y0=-1.
①若k≠0,则kCF=-$\frac{1}{k}$,
∴kAB•kCF=-1,
∴$\overrightarrow{AB}$•$\overrightarrow{CF}$=0;
②若k=0,$\overrightarrow{CF}$=(-2k,2),$\overrightarrow{AB}$=(x2-x1,k(x2-x1)),$\overrightarrow{AB}•\overrightarrow{CF}$=-2k(x2-x1)+2k(x2-x1)=0,
∴$\overrightarrow{AB}$•$\overrightarrow{CF}$=0;
(2)解:由(1)知,点C到AB的距离d=|CF|=2$\sqrt{1+{k}^{2}}$,
|AB|=|AF|+|FB|=y1+y2+2=k(x1+x2)+4=4k2+4,
∴$S=\frac{1}{2}|AB|•d$=$4({k}^{2}+1)^{\frac{3}{2}}$,
∴当k=0时,△ABC的面积的最小值为4.
点评 本题考查了抛物线的定义及其标准方程及其性质、利用导数研究抛物线的切线、向量垂直与数量积的关系、三角形面积计算公式,考查了推理能力与计算能力,属于难题.

| A. | 8 | B. | -8 | C. | 8或-8 | D. | 都不对 |
| A. | 命题“若m>0,则方程x2+x-m=0有实数根”的逆否命题是“若方程x2+x-m=0没有实数根,则m≤0” | |
| B. | “x=1”是“x2-3x+2=0”的充分不必要条件 | |
| C. | 命题“若xy=0,则x,y中至少有一个为0”的否命题是“若xy≠0,则x,y中至多有一个为0” | |
| D. | 对于命题p:?x∈R,使x2+x+1<0;则¬p:?x∈R,均有x2+x+1≥0 |
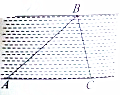 如图,在河岸边有一点A,河对岸有一点B,要测量A,B两点的距离,现在岸边取基线AC,测得AC=120m,∠BAC=45°,∠BCA=75°,求A,B两点间的距离.
如图,在河岸边有一点A,河对岸有一点B,要测量A,B两点的距离,现在岸边取基线AC,测得AC=120m,∠BAC=45°,∠BCA=75°,求A,B两点间的距离.