题目内容
18.已知A为椭圆$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}$=1上的动点,MN为圆(x-1)2+y2=1的一条直径,则AM•AN的最大值为15.分析 由题意画出图形,得到椭圆上离圆心最远的点A,在设出圆的直径两端点的坐标,由平面向量数量积运算求得答案.
解答 解:如图,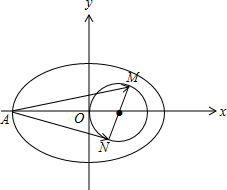
圆(x-1)2+y2=1在椭圆内,椭圆上的所有点只有左顶点到圆心(1,0)距离最远,
由题意可设圆的直径的两个端点为M(1+cosθ,sinθ),N(1-cosθ,-sinθ),
又A(-3,0),
∴$\overrightarrow{AM}$=(4+cosθ,sinθ),$\overrightarrow{AN}$=(4-cosθ,-sinθ),
则$\overrightarrow{AM}$•$\overrightarrow{AN}$=16-cos2θ-sin2θ=15.
∴AM•AN的最大值为15.
故答案为:15.
点评 本题考查椭圆的简单性质,考查了平面向量的数量积运算,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
3.已知角α的终边过点P(-4m,3m)(m<0),则2sinα+cosα的值是( )
| A. | 1 | B. | $\frac{2}{5}$ | C. | -$\frac{2}{5}$ | D. | -1 |
9.下列不等式中成立的是( )
| A. | $sin(-\frac{π}{18})<sin(-\frac{π}{10})$ | B. | $sin\frac{5π}{3}>sin2$ | ||
| C. | $cos(-\frac{23}{5}π)>cos(-\frac{17}{4}π)$ | D. | $tan(-\frac{π}{5})>tan(-\frac{3π}{7})$ |
6.两次购买同一种物品,可以用两种不同的策略,第一种是不考虑物品价格的升降,每次购买这种物品数量一定;第二种是不考虑物品价格的升降,每次购买这种物品所花的钱数一定,哪种购物方式比较经济( )
| A. | 第一种 | B. | 第二种 | C. | 都一样 | D. | 不确定 |
3.如表是某厂1~4月份用水量(单位:百吨)的一组数据:
由散点图可知,用水量y与月份x之间有较好的线性相关关系,其回归直线方程是$\stackrel{∧}{y}$=-2x+$\stackrel{∧}{a}$,则$\stackrel{∧}{a}$等于8.5.
| 月份x | 1 | 2 | 3 | 4 |
| 用水量y | 4.5 | 4 | 3 | 2.5 |
10.函数f(x)=ax3-x2+x-6在(-∞,+∞)上既有极大值又有极小值,则a的取值范围为( )
| A. | a>0 | B. | a<0 | C. | $a>\frac{1}{3}$ | D. | $a<\frac{1}{3}$且a≠0 |