题目内容
设函数 .
.
若 是函数
是函数 的极值点,1和
的极值点,1和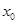 是函数
是函数 的两个不同零点,且
的两个不同零点,且 ,求
,求 .
.
若对任意 ,都存在
,都存在 (
( 为自然对数的底数),使得
为自然对数的底数),使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(1)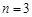 ;(2)
;(2)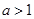 .
.
解析试题分析:(1)对零点存在性定理的考查,借助 是极值及1是零点建立两个方程解出
是极值及1是零点建立两个方程解出 和
和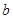 ,然后对函数
,然后对函数 进行求导定出其单调性,再利用零点存在性定理尝试算出
进行求导定出其单调性,再利用零点存在性定理尝试算出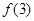 和
和 ,发现异号,得出零点所在的区间;(2)首先需要我们将两个变量的不等式恒成立问题转化成常见的一个变量的不等式有解问题,然后再构造这个不等式为函数
,发现异号,得出零点所在的区间;(2)首先需要我们将两个变量的不等式恒成立问题转化成常见的一个变量的不等式有解问题,然后再构造这个不等式为函数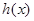 ,为了找
,为了找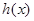 的最小值并且让其小于0,我们利用试根法试出
的最小值并且让其小于0,我们利用试根法试出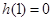 ,然后只要让
,然后只要让 右零点在端点1右边即可,解出范围.
右零点在端点1右边即可,解出范围.
试题解析:(1)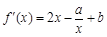 ,∵
,∵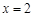 是函数
是函数 的极值点,∴
的极值点,∴ .∵1是函数
.∵1是函数 的零点,得
的零点,得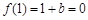 ,由
,由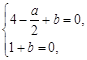 解得
解得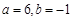 . ∴
. ∴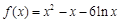 ,
,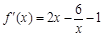 ,
,
令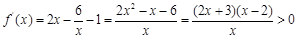 ,
,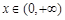 ,得
,得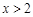 ; 令
; 令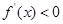 得
得 ,所以
,所以 在
在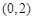 上单调递减;在
上单调递减;在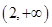 上单调递增.故函数
上单调递增.故函数 至多有两个零点,其中
至多有两个零点,其中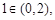
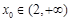 ,因为
,因为 ,
,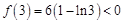 ,
,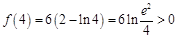 ,所以
,所以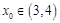 ,故
,故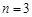 .
.
(2)令 ,
,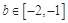 ,则
,则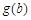 为关于
为关于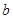 的一次函数且为增函数,根据题意,对任意
的一次函数且为增函数,根据题意,对任意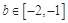 ,都存在
,都存在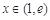 ,使得
,使得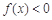 成立,则
成立,则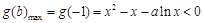 在
在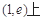 有解,令
有解,令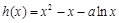 ,只需存在
,只需存在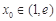 使得
使得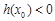 即可,
即可,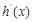 =
=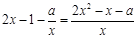 ,令
,令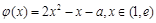 ,∵
,∵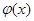 的两个零点分布在
的两个零点分布在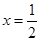 左右,又∵
左右,又∵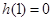 ,∴
,∴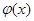 的右零点必须大于1,∴
的右零点必须大于1,∴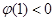 ,解得
,解得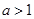 .综上所述,当
.综上所述,当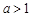 时,对任意
时,对任意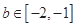 ,都存在
,都存在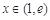 ,使得
,使得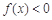 成立.
成立.
考点:1.零点存在性定理;2.根的分布.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
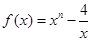 ,且
,且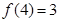 .
. 的奇偶性并说明理由;
的奇偶性并说明理由;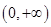 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;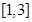 上,不等式
上,不等式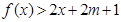 恒成立,试确定实数
恒成立,试确定实数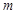 的取值范围.
的取值范围. ,
, ,其中
,其中 且
且 .
. ,求函数
,求函数 的单调递增区间;
的单调递增区间; 时,函数
时,函数 有极值,求函数
有极值,求函数 (
( 是自然对数的底数),是否存在a使
是自然对数的底数),是否存在a使 在
在 上为减函数,若存在,求实数a的范围;若不存在,请说明理由.
上为减函数,若存在,求实数a的范围;若不存在,请说明理由. .
. 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围. ,若
,若 的最小值是
的最小值是 ,求函数
,求函数 .
. ,求
,求 的极值;
的极值; 的取值范围.
的取值范围. ,(
,( 且
且 ).
). ,令
,令 ,试判断函数
,试判断函数 在
在 上的单调性并证明你的结论;
上的单调性并证明你的结论; 且
且
 的定义域和值域都是
的定义域和值域都是 的最大值;
的最大值; 对
对 恒成立,求实数
恒成立,求实数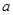 的取值范围;
的取值范围;
 在
在 是增函数,求
是增函数,求 的取值范围;
的取值范围; ,对于函数
,对于函数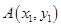 ,
, ,其中
,其中 ,直线
,直线 的斜率为
的斜率为 ,记
,记 ,若
,若 求证:
求证: .
. (a≠0)在(0,
(a≠0)在(0, )内有极值.
)内有极值.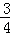 .
.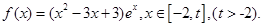
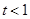 时,求函数
时,求函数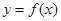 的单调区间;
的单调区间;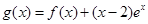 ,试问函数
,试问函数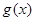 在
在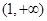 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.