题目内容
等差数列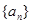 的前
的前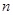 项和记为
项和记为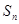 ,若
,若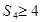 ,
,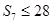 ,则
,则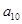 的最大值为 .
的最大值为 .
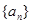 的前
的前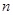 项和记为
项和记为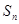 ,若
,若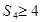 ,
,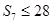 ,则
,则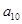 的最大值为 .
的最大值为 .16
试题分析:
 等差数列
等差数列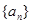 的前
的前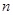 项和为
项和为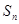 ,
,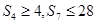 ,
,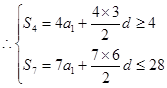 ,即
,即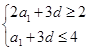 ,
,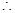
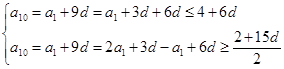 ,
,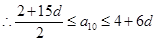 ,
,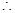
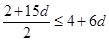 ,解得
,解得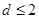 ,
,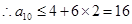 .
.
练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
题目内容
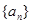 的前
的前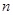 项和记为
项和记为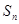 ,若
,若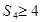 ,
,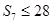 ,则
,则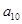 的最大值为 .
的最大值为 .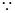 等差数列
等差数列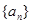 的前
的前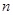 项和为
项和为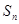 ,
,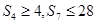 ,
,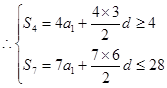 ,即
,即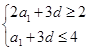 ,
,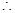
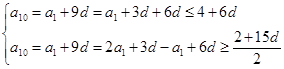 ,
,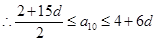 ,
,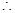
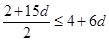 ,解得
,解得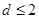 ,
,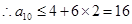 .
.
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案