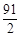题目内容
数列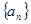 是递增的等差数列,且
是递增的等差数列,且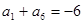 ,
, .
.
(1)求数列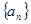 的通项公式;
的通项公式;
(2)求数列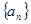 的前
的前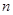 项和
项和 的最小值;
的最小值;
(3)求数列 的前
的前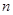 项和
项和 .
.
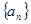 是递增的等差数列,且
是递增的等差数列,且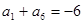 ,
, .
.(1)求数列
 的通项公式;
的通项公式;(2)求数列
 的前
的前 项和
项和 的最小值;
的最小值;(3)求数列
 的前
的前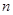 项和
项和 .
.(1) 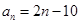 ;(2)
;(2)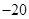 ;(3)
;(3)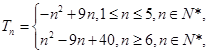 .
.
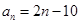 ;(2)
;(2)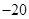 ;(3)
;(3)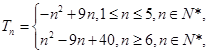 .
.试题分析:(1)这是等差数列的基础题型,可直接利用基本量(列出关于
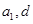 的方程组)求解,也可利用等差数列的性质
的方程组)求解,也可利用等差数列的性质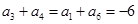 ,这样可先求出
,这样可先求出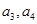 ,然后再求出
,然后再求出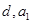 ,得通项公式;(2)等差数列的前
,得通项公式;(2)等差数列的前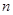 和
和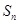 是关于
是关于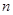 的二次函数的形式,故可直接求出
的二次函数的形式,故可直接求出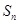 ,然后利用二次函数的知识得到最小值,当然也可根据数列的特征,本题等差数列是首项为负且递增的数列,故可求出符合
,然后利用二次函数的知识得到最小值,当然也可根据数列的特征,本题等差数列是首项为负且递增的数列,故可求出符合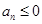 的
的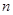 的最大值,这个最大值
的最大值,这个最大值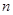 就使得
就使得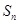 最小(如果
最小(如果 ,则
,则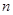 和
和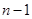 都使
都使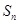 最小);(3)由于
最小);(3)由于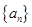 前几项为负,后面全为正,故分类求解(目的是根据绝对值定义去掉绝对值符号),特别是
前几项为负,后面全为正,故分类求解(目的是根据绝对值定义去掉绝对值符号),特别是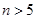 时,
时,
 ,这样可利用第(2)题的结论快速得出结论.
,这样可利用第(2)题的结论快速得出结论.试题解析:(1) 由

 ,得
,得 、
、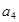 是方程
是方程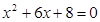 的二个根,
的二个根,
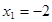 ,
, ,此等差数列为递增数列,
,此等差数列为递增数列,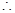
 ,
,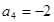 ,公差
,公差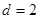 ,
,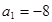 .
.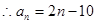 4分
4分(2)
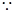
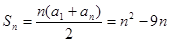 ,
,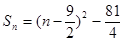 ,
,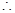
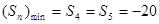 8分
8分(3)由
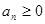 得
得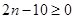 ,解得
,解得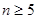 ,此数列前四项为负的,第五项为0,从第六项开始为正的. 10分
,此数列前四项为负的,第五项为0,从第六项开始为正的. 10分当
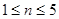 且
且 时,
时,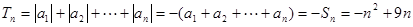 . 12分
. 12分当
 且
且 时,
时,
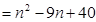 . 14分
. 14分 项和公式;(3)绝对值与分类讨论.
项和公式;(3)绝对值与分类讨论.
练习册系列答案
相关题目
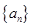 的前
的前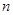 项和为
项和为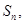 记
记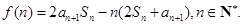
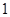 的等差数列,求
的等差数列,求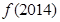 ;
; 且数列
且数列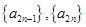 均是公比为
均是公比为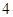 的等比数列,
的等比数列,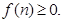
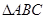 的三边长
的三边长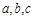 ,满足
,满足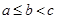
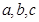 均为正整数,且
均为正整数,且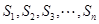 ,且
,且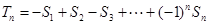 ,求满足不等式
,求满足不等式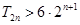 的所有
的所有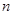 的值;
的值;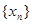 满足
满足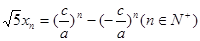 ,证明数列
,证明数列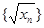 中的任意连续三项为边长均可以构成直角三角形,且
中的任意连续三项为边长均可以构成直角三角形,且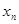 是正整数.
是正整数.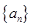 的前
的前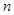 项和为
项和为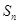 ,且满足
,且满足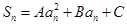 ,其中
,其中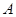 、
、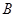 、
、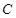 是常数.
是常数.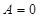 ,
,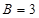 ,
,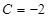 ,求数列
,求数列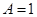 ,
,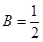 ,
,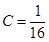 ,且
,且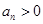 ,求数列
,求数列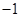 的等比数列.
的等比数列.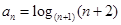
 .我们把使乘积
.我们把使乘积 为整数的数n叫做“优数”,则在区间(1,2004)内的所有优数的和为( )
为整数的数n叫做“优数”,则在区间(1,2004)内的所有优数的和为( )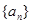 的前
的前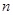 项和记为
项和记为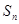 ,若
,若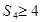 ,
,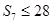 ,则
,则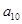 的最大值为 .
的最大值为 .