题目内容
(本小题满分12分)已知函数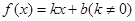 的图象与
的图象与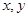 轴分别相交于点
轴分别相交于点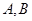 两点,向量
两点,向量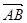
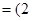 ,
,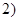 ,又函数
,又函数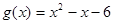 ,且
,且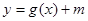 的值域是
的值域是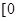 ,
,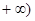 。
。
(1)求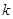 ,
,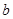 及
及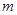 的值;(2)当
的值;(2)当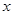 满足
满足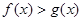 时,求函数
时,求函数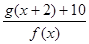 的最小值。
的最小值。
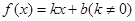 的图象与
的图象与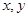 轴分别相交于点
轴分别相交于点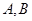 两点,向量
两点,向量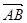
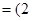 ,
,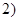 ,又函数
,又函数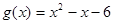 ,且
,且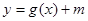 的值域是
的值域是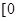 ,
,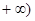 。
。(1)求
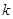 ,
,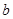 及
及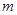 的值;(2)当
的值;(2)当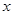 满足
满足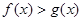 时,求函数
时,求函数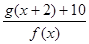 的最小值。
的最小值。(1)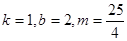 (2)3
(2)3
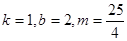 (2)3
(2)3试题分析:(1)因为函数
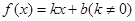 的图象与
的图象与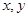 轴分别相交于点
轴分别相交于点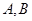 两点,
两点,分别令
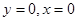 得
得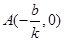 ,
,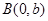 ,则
,则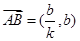 ,
,又因为
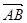
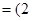 ,
,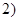 ,
,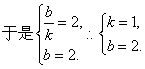 ……4分
……4分又
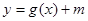
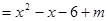 的值域是
的值域是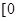 ,
,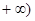 ,
,所以
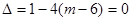 ,解得
,解得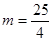 ,
,所以
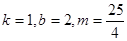 . ……6分
. ……6分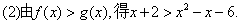
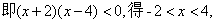
所以
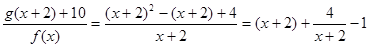 ,
,因为
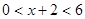 ,所以
,所以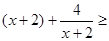 4,
4,当且仅当
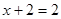 时等号成立,
时等号成立,所以
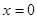 时,
时,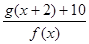 的最小值是3. ……12分
的最小值是3. ……12分点评:利用基本不等式求最值时,一正二定三相等三个条件缺一不可,而且还要写清楚取等号的条件.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
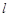 与两坐标轴围成的三角形的面积为3,分别求满足下列条件的直线
与两坐标轴围成的三角形的面积为3,分别求满足下列条件的直线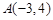 .
.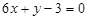 垂直.
垂直.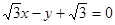 与
与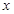 轴,
轴,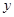 轴分别相交于A、B两点,以AB为边做等边
轴分别相交于A、B两点,以AB为边做等边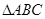 ,若平面内有一点
,若平面内有一点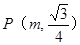 使得
使得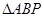 与
与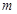 的值.
的值.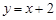 上的一点向圆
上的一点向圆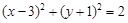 引切线,则切线长的最小值为
引切线,则切线长的最小值为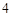
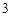
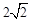
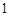
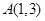 关于直线
关于直线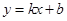 的对称点是
的对称点是 ,则直线
,则直线 轴上的截距是( )
轴上的截距是( )



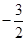
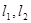 的倾斜角分别为
的倾斜角分别为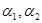 ,则下列四个命题中正确的是( )
,则下列四个命题中正确的是( ) ,则两直线的斜率:
,则两直线的斜率: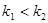
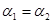 ,则两直线的斜率:
,则两直线的斜率: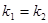
 关于点
关于点 对称的直线
对称的直线 的方程是______________.
的方程是______________.