题目内容
7．在△ABC，内角A，B，C的对边分别为a，b，c，若$\frac{cosA-2cosC}{cosB}$=$\frac{2c-a}{b}$，则$\frac{sinC}{sinA}$=2．分析 利用正弦定理可得：$\frac{cosA-2cosC}{cosB}$=$\frac{2sinC-sinA}{sinB}$，整理后由两角和的正弦函数公式即可得解．
解答 解：在△ABC中，由 $\frac{cosA-2cosC}{cosB}$=$\frac{2c-a}{b}$，
利用正弦定理可得 $\frac{cosA-2cosC}{cosB}$=$\frac{2sinC-sinA}{sinB}$，
∴sinBcosA-2cosCsinB=2sinCcosB-sinAcosB，
∴sinBcosA+cosBsinA=2（sinBcosC+cosBsinC），
∴sin（B+A）=2sin（B+C），即 sinC=2sinA，则 $\frac{sinC}{sinA}=2$，
故答案为：2．
点评 本题主要考查了正弦定理，两角和的正弦函数公式的应用，属于基本知识的考查．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
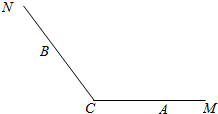已知点A，B分别在射线CM，CN（不含端点C）上运动，∠MCN=$\frac{2π}{3}$，在△ABC中，角A，B，C所对的边分别是a，b，c