题目内容
（本小题满分10分）
选修4—1：几何证明选讲
如图，AB是⊙O的直径，C，F为⊙O上的点，CA是∠BAF的角平分线，过点C作
CD⊥AF交AF的延长线于D点，CM⊥AB，垂足为点M.
（1）求证：DC是⊙O的切线；
（2）求证：AM·MB=DF·DA.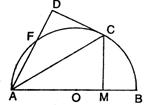
选修4—1：几何证明选讲
如图，AB是⊙O的直径，C，F为⊙O上的点，CA是∠BAF的角平分线，过点C作
CD⊥AF交AF的延长线于D点，CM⊥AB，垂足为点M.
（1）求证：DC是⊙O的切线；
（2）求证：AM·MB=DF·DA.
略
选修4—1：几何证明选讲
解：（I）连结OC，∴∠OAC=∠OCA，又∵CA是∠BAF的角平分线，
∴∠OAC=∠FAC，
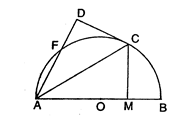∴∠FAC=∠ACO，∴OC∥AD.………………3分
∵CD⊥AF，
∴CD⊥OC，即DC是⊙O的切线.…………5分
（Ⅱ）连结BC，在Rt△ACB中，
CM⊥AB，∴CM2=AM·MB.
又∵DC是⊙O的切线，∴DC2=DF·DA.
易知△AMC≌△ADC，∴DC=CM，
∴AM·MB=DF·DA…………10分
解：（I）连结OC，∴∠OAC=∠OCA，又∵CA是∠BAF的角平分线，
∴∠OAC=∠FAC，
∴∠FAC=∠ACO，∴OC∥AD.………………3分∵CD⊥AF，
∴CD⊥OC，即DC是⊙O的切线.…………5分
（Ⅱ）连结BC，在Rt△ACB中，
CM⊥AB，∴CM2=AM·MB.
又∵DC是⊙O的切线，∴DC2=DF·DA.
易知△AMC≌△ADC，∴DC=CM，
∴AM·MB=DF·DA…………10分
练习册系列答案
相关题目
.
；
；
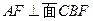几何体分成的两个锥体的体积分别为
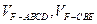，求
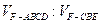的值.
（ ）
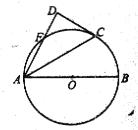
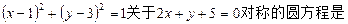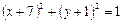
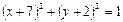
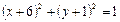
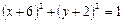
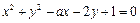关于直线x – y – 1 = 0对称的圆的方程是
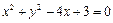，则a的值等于（ ）
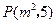与圆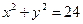
的位置关系是（ ）
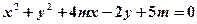表示圆的充要条件是（ ）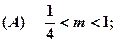
； 
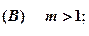
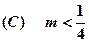