题目内容

16．函数y=|x+2|在区间[-3，0]上是（　　）
A．减函数B．增函数C．先减后增D．先增后减

分析 结合一次函数的图象和性质，分段讨论各段上函数的单调性，综合讨论结果，可得答案．

解答 解：当x∈[-3，-2]时，y=|x+2|=-x-2为减函数，
当x∈[-2，0]时，y=|x+2|=x+2为增函数，
故函数y=|x+2|在区间[-3，0]上是先减后增，
故选：C

点评 本题考查的知识点是分段函数的单调性，分段函数分段处理，是解答分段函数的基本方法．

练习册系列答案
相关题目
6．已知全集U=R．，A={x|-4≤x＜2}，B={x|-1＜x≤3}，P={x|x≤0或x≥$\frac{5}{2}$}，求A∩B，（∁UB）∪P，（A∩B）∩（∁UP）
7．函数f（x）=ax2+bx+3x+b是{a-3，2a]上的偶函数，则f（1）=-2．
4．将指数函数f（x）的图象按向量$\overrightarrow{a}$=（1，0）平移后得到图示，则f-1（x）=（　　）
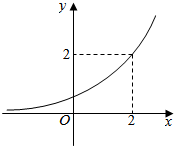
A．log2xB．3log2xC．log3xD．2log3x
11．求证：函数f（x）=-x2+2在（-∞，0）上是增函数．
1．函数f（x）=$\left\{\begin{array}{l}{x+1，x≥0}\\{x-1，x＜0}\end{array}\right.$ 在R上是（　　）
A．减函数B．增函数C．先减后增D．无单调性
8．已知函数f（x）=|2x+1|+||x-1|．
（1）解不等式f（x）＜2；
（2）设函数g（x）=log2（|2x+1|+||x-1|-a）的定义域为全体实数R，求实数a的取值范围；当值域是全体实数R时，求出实数a取值范围．
5．根据下列圆的标准方程，分别求出圆心的坐标与半径，并画出图形．
（1）（x+1）2+y2=4；
（2）x2+（y+2）2=3．
12．某班元旦联欢会举行抽奖活动，现有六张分别标有1，2，3，4，5，6六个数字的形状相同的卡片，其中标有偶数数字的卡片是有奖卡片，且奖品个数与卡片上所标数字相同，抽奖规则如下：每人每次抽取的两张卡片．
（1）若甲、乙两位同学抽奖相互独立，求甲、乙两位同学所得奖品个数都不少于4的概率；
（2）记甲同学所得奖品个数为随机变量X，求X分布列及数学期望．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网