题目内容
【题目】已知△ABC的角A、B、C所对的边分别是a、b、c，设向量 
， 
， 
．
（1）若 
∥ 
，求证：△ABC为等腰三角形；
（2）若 ⊥ 
，边长c=2，角C= 
，求△ABC的面积．
【答案】
（1）证明：∵m∥n
∴asinA=bsinB
即a 
=b 
．其中R为△ABC外接圆半径．
∴a=b
∴△ABC为等腰三角形
（2）证明：由题意，mp=0
∴a（b﹣2）+b（a﹣2）=0
∴a+b=ab
由余弦定理4=a2+b2﹣2abcos 
∴4=a2+b2﹣ab=（a+b）2﹣3ab
∴（ab）2﹣3ab﹣4=0
∴ab=4或ab=﹣1（舍去）
∴S△ABC= 
absinC
= ×4×sin = 
【解析】（1）利用向量平行的条件，写出向量平行坐标形式的条件，得到关于三角形的边和角之间的关系，利用余弦定理变形得到三角形是等腰三角形．（2）利用向量垂直数量积为零，写出三角形边之间的关系，结合余弦定理得到求三角形面积所需的两边的乘积的值，求出三角形的面积．
练习册系列答案
阅读快车系列答案
相关题目
【题目】为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有800名学生参加了这次竞赛．为了解本次竞赛成绩情况，从中抽取了部分学生的成绩进行统计． 请你根据尚未完成并有局部污损的频率分布表和频率分布直方图，解答下列问题：
分组 | 频数 | 频率 |
50.5～60.5 | 6 | 0.08 |
60.5～70.5 | 0.16 | |
70.5～80.5 | 15 | |
80.5～90.5 | 24 | 0.32 |
90.5～100.5 | ||
合计 | 75 | 1.00 |
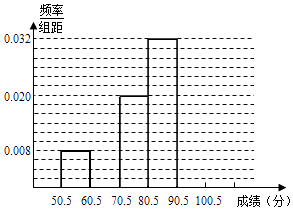
（1）填充频率分布表的空格；
（2）补全频率分布直方图；
（3）根据频率分布直方图求此次“环保知识竞赛”的平均分为多少？
