题目内容
【题目】已知函数![]() .
.
(1)若![]() 的最大值为
的最大值为![]() ,求
,求![]() 的值;
的值;
(2)若存在实数![]() 且
且![]() ,使得
,使得![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)对函数进行求导,然后根据![]() 的正负性进行分类讨论求出函数的单调性,最后根据题意求出
的正负性进行分类讨论求出函数的单调性,最后根据题意求出![]() 的值;
的值;
(2)根据题意和(1)可以判断出函数的单调性,进而可以确定![]() 介于
介于![]() 之间,不妨设
之间,不妨设![]() ,这样根据函数的单调性和绝对值的性质进行求解即可.
,这样根据函数的单调性和绝对值的性质进行求解即可.
(1)![]() ,若
,若![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,![]() 无最值,不合题意;若
无最值,不合题意;若![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,故
上单调递减,故![]() 的最大值
的最大值![]() ,解得
,解得![]() ,符合题意.
,符合题意.
综上,![]() .
.
(2)若![]() ,则由(1)知
,则由(1)知![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.若存在实数
上单调递减.若存在实数![]() ,使得
,使得![]() ,则
,则![]() 介于
介于![]() 之间,不妨设
之间,不妨设![]() ,因为
,因为![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,且
上单调递减,且![]() ,所以当
,所以当![]() 时,
时,![]() ,由
,由![]() ,可得
,可得![]() ,故
,故![]() ,又
,又![]() 在
在![]() 上递增,且
上递增,且![]() ,
,
所以![]() ,所以
,所以![]() ,
,
同理![]() .所以
.所以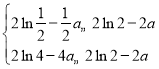 ,解得
,解得![]() ,不等式得证.
,不等式得证.

【题目】2020年3月,各行各业开始复工复产,生活逐步恢复常态,某物流公司承担从甲地到乙地的蔬菜运输业务.已知该公司统计了往年同期200天内每天配送的蔬菜量X(40≤X<200,单位:件.注:蔬菜全部用统一规格的包装箱包装),并分组统计得到表格如表:
蔬菜量X | [40,80) | [80,120) | [120,160) | [160,200) |
天数 | 25 | 50 | 100 | 25 |
若将频率视为概率,试解答如下问题:
(1)该物流公司负责人决定随机抽出3天的数据来分析配送的蔬菜量的情况,求这3天配送的蔬菜量中至多有2天小于120件的概率;
(2)该物流公司拟一次性租赁一批货车专门运营从甲地到乙地的蔬菜运输.已知一辆货车每天只能运营一趟,每辆货车每趟最多可装载40件,满载才发车,否则不发车.若发车,则每辆货车每趟可获利2000元;若未发车,则每辆货车每天平均亏损400元.为使该物流公司此项业务的营业利润最大,该物流公司应一次性租赁几辆货车?