题目内容
【题目】已知矩形ABCD的边AB=a,BC=3,PA⊥平面ABCD,若BC边上有且只有一点M,使PM⊥DM,则a的值为
【答案】1.5
【解析】解:∵PA⊥平面ABCD,
∴PA⊥DM,
若BC边上存在点M,使PM⊥MD,
则DM⊥面PAM,
即DM⊥AM,
∴以AD为直径的圆和BC相交即可.
∵AD=BC=3,
∴圆的半径为3,
要使线段BC和半径为3的圆相切,
则AB=1.5,
即a=1.5,
∴a的值是1.5.
所以答案是:1.5.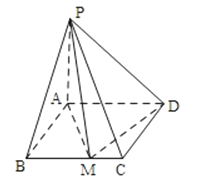
【考点精析】本题主要考查了直线与平面垂直的判定的相关知识点,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.

练习册系列答案
相关题目