题目内容
(能力挑战题)已知f(x)为R上的可导函数,且?x∈R,均有f(x)>f′(x),则有( )
| A.e2014f(-2014)<f(0),f(2014)>e2014f(0) |
| B.e2014f(-2014)<f(0),f(2014)<e2014f(0) |
| C.e2014f(-2014)>f(0),f(2014)>e2014f(0) |
| D.e2014f(-2014)>f(0),f(2014)<e2014f(0) |
D
构造函数g(x)=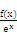 ,
,
则g′(x)=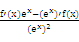 =
=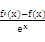 .
.
因为?x∈R,均有f(x)>f′(x),并且ex>0,
所以g′(x)<0,故函数g(x)=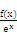 在R上单调递减,
在R上单调递减,
所以g(-2014)>g(0),g(2014)<g(0),
即 >f(0),
>f(0),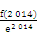 <f(0),
<f(0),
也就是e2014f(-2014)>f(0),f(2014)<e2014f(0),故选D.
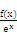 ,
,则g′(x)=
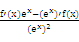 =
=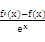 .
.因为?x∈R,均有f(x)>f′(x),并且ex>0,
所以g′(x)<0,故函数g(x)=
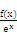 在R上单调递减,
在R上单调递减,所以g(-2014)>g(0),g(2014)<g(0),
即
 >f(0),
>f(0),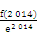 <f(0),
<f(0),也就是e2014f(-2014)>f(0),f(2014)<e2014f(0),故选D.

练习册系列答案
相关题目
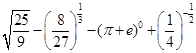 ; ②
; ②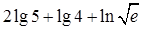 .
. 有两个不等实根,则实数
有两个不等实根,则实数 的取值范围是( )
的取值范围是( )



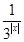 .
.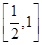 恒成立,求m的取值范围.
恒成立,求m的取值范围. ,若
,若 ,且
,且 ,则
,则 的最小值为( ).
的最小值为( ).

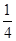 ,最大值与最小值之积为-
,最大值与最小值之积为-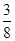 ,则a的值为( )
,则a的值为( )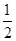
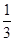
 的图象与函数
的图象与函数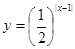
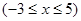 的图象所有交点的横坐标之和等于( )
的图象所有交点的横坐标之和等于( )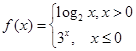 ,且函数
,且函数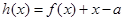 有且只有一个零点,则实数
有且只有一个零点,则实数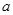 的取值范围是( )
的取值范围是( )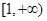 B.
B.
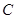 .
.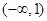 D.
D.