Question

在数列{an}和等比数列{bn}中，a1＝0，a3＝2，bn＝2an＋1(n∈N*)．

(1)求数列{bn}及{an}的通项公式；

(2)若cn＝an·bn，求数列{cn}的前n项和Sn.

 

Answer 1

（1）an＝n－1（2）Sn＝4＋(n－2)·2n＋1

【解析】(1)方法一，依题意b1＝2，b3＝23＝8，

设数列{bn}的公比为q，由bn＝2an＋1>0，可知q>0.

由b3＝b1·q2＝2·q2＝8，得q2＝4，又q>0，则q＝2，

故bn＝b1qn－1＝2·2n－1＝2n，

又由2an＋1＝2n，得an＝n－1.

(2)依题意cn＝(n－1)·2n.

Sn＝0·21＋1·22＋2·23＋…＋(n－2)·2n－1＋(n－1)·2n ，①

则2Sn＝0·22＋1·23＋2·24＋…＋(n－2)·2n＋(n－1)·2n＋1，②

①－②得

－Sn＝22＋23＋…＋2n－(n－1)·2n＋1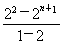＝－(n－1)·2n＋1，

即－Sn＝－4＋(2－n)·2n＋1，故Sn＝4＋(n－2)·2n＋1.

方法二，(1)依题意{bn}为等比数列，则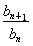＝q(常数)，

由bn＝2an＋1>0，可知q>0.

由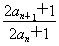＝2an＋1－an＝q，

得an＋1－an＝log2q(常数)，故{an}为等差数列．

设{an}的公差为d，由a1＝0，a3＝a1＋2d＝0＋2d＝2，得d＝1，

故an＝n－1.

(2)同方法一．