题目内容
12．已知函数y=x2m+1在区间（0，+∞）上是增函数，求实数m的取值范围．分析 利用幂函数的性质，列出不等式，然后求解m的取值范围．
解答 解：函数y=x2m+1在区间（0，+∞）上是增函数，
可得2m+1＞0，解得m$＞-\frac{1}{2}$．
实数m的取值范围：（-$\frac{1}{2}$，+∞）．
点评 本题考查幂函数简单性质的应用，考查计算能力．
练习册系列答案
相关题目
3．下列函数中，在区间（0，+∞）上为增函数的是（ ）
| A． | y=log2（x+5） | B． | $y={（{\frac{1}{3}}）^x}$ | C． | y=-$\sqrt{x+2}$ | D． | y=$\frac{1}{x}$-x |
7．设函数f（x）=$\left\{\begin{array}{l}{asinx+2，x≥0}\\{{x}^{2}+2a，x＜0}\end{array}\right.$（其中a∈R）的值域为S，若[1，+∞）⊆S，则a的取值范围是（ ）
| A． | （-∞，$\frac{1}{2}$） | B． | [1，$\frac{3}{2}$]∪（$\frac{7}{4}$，2] | C． | （-∞，$\frac{1}{2}$）∪[1，2] | D． | （$\frac{3}{2}$，+∞） |
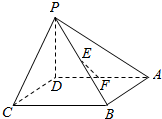如图，在四棱锥P-ABCD中，底面ABCD为正方形，PD⊥平面ABCD，且PD=AB=2a，E是PB的中点，F是AD的中点，求证：EF⊥平面PCB．
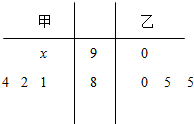如图用茎叶图记录了同班的甲、乙两名学生4次数学考试成绩，其中甲的一次成绩模糊不清，用x标记．