Question

【题目】在平面四边形ACBD（图①）中，△ABC与△ABD均为直角三角形且有公共斜边AB，设AB=2，∠BAD=30°，∠BAC=45°，将△ABC沿AB折起，构成如图②所示的三棱锥C′﹣ABC，且使 ．
（Ⅰ）求证：平面C′AB⊥平面DAB；
（Ⅱ）求二面角A﹣C′D﹣B的余弦值．

Answer 1

【答案】解：（Ⅰ）取AB的中点O，连C′O，DO，
在RT△ACB，RT△ADB，AB=2，则C′O=DO=1，又，∴C′O2+DO2=C′D2 ， 即C′O⊥OD，
又，AB∩OD=O，AB，OD平面ABD∴C′O⊥平面ABD，
又C′O平面ABC′∴平面C′AB⊥平面DAB
（Ⅱ）以O为原点，AB，OC′所在的直线分别为y，z轴，建立如图空间直角坐标系，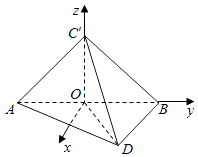

则 ，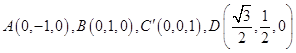
∴
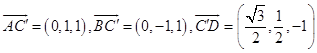
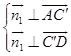设平面AC′D的法向量为 ，则 ，即 ，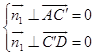
，
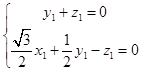令z1=1，则y1=﹣1， ，∴
设平面BC′D的法向量为 ，则 ，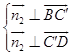
即 ， ，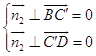
令z2=1，则y2=1， ，∴
∴ ，
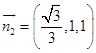
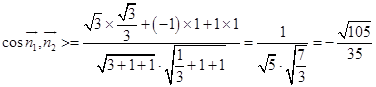二面角A﹣C′D﹣B的余弦值为
【解析】（Ⅰ）取AB的中点O，连C′O，DO，通过就是证明C′O⊥OD，证明C′O⊥平面ABD，然后证明平面C′AB⊥平面DAB．（Ⅱ）以O为原点，AB，OC′所在的直线分别为y，z轴，建立如图空间直角坐标系，
求出平面AC′D的法向量，平面BC′D的法向量，利用向量的数量积求解二面角A﹣C′D﹣B的余弦值．
【考点精析】关于本题考查的平面与平面垂直的判定，需要了解一个平面过另一个平面的垂线，则这两个平面垂直才能得出正确答案．