题目内容
已知圆C的方程为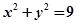 ,点A
,点A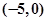 ,直线
,直线 :
: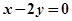
(1)求与圆C相切,且与直线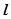 垂直的直线方程;
垂直的直线方程;
(2)O为坐标原点,在直线OA上是否存在异于A点的B点,使得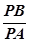 为常数,若存在,求出点B,不存在说明理由.
为常数,若存在,求出点B,不存在说明理由.
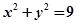 ,点A
,点A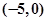 ,直线
,直线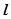 :
: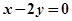
(1)求与圆C相切,且与直线
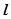 垂直的直线方程;
垂直的直线方程;(2)O为坐标原点,在直线OA上是否存在异于A点的B点,使得
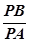 为常数,若存在,求出点B,不存在说明理由.
为常数,若存在,求出点B,不存在说明理由.(1)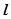 :
: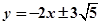 ;(2)存在点B
;(2)存在点B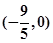 对于圆上任意一点P都有
对于圆上任意一点P都有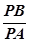 为常数
为常数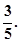
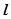 :
: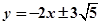 ;(2)存在点B
;(2)存在点B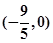 对于圆上任意一点P都有
对于圆上任意一点P都有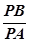 为常数
为常数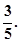
(1)因为所求直线与l垂直,所以可设l: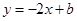 ,然后再根据直线l与圆C相切,圆心C到直线l的距离等于等于圆的半径3,可建立关于b的方程,求出b的值.
,然后再根据直线l与圆C相切,圆心C到直线l的距离等于等于圆的半径3,可建立关于b的方程,求出b的值.
(2)假设存在这样的点B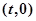 ,使得
,使得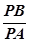 为常数
为常数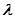 ,则
,则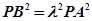
即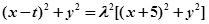 再根据
再根据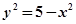 ,
,
可转化为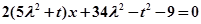 对任意
对任意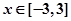 恒成立问题来解决即可.
恒成立问题来解决即可.
解:(1)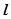 :
: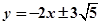
(2)假设存在这样的点B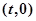 ,使得
,使得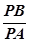 为常数
为常数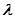 ,则
,则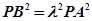
即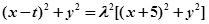 ……①,又
……①,又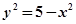 ……②
……②
由①②可得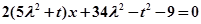 对任意
对任意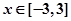 恒成立
恒成立
所以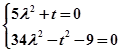 解得
解得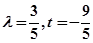 或
或 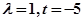 (舍去)
(舍去)
所以存在点B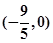 对于圆上任意一点P都有
对于圆上任意一点P都有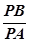 为常数
为常数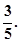
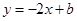 ,然后再根据直线l与圆C相切,圆心C到直线l的距离等于等于圆的半径3,可建立关于b的方程,求出b的值.
,然后再根据直线l与圆C相切,圆心C到直线l的距离等于等于圆的半径3,可建立关于b的方程,求出b的值.(2)假设存在这样的点B
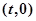 ,使得
,使得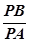 为常数
为常数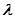 ,则
,则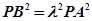
即
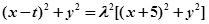 再根据
再根据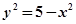 ,
,可转化为
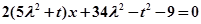 对任意
对任意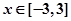 恒成立问题来解决即可.
恒成立问题来解决即可.解:(1)
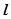 :
: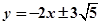
(2)假设存在这样的点B
 ,使得
,使得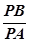 为常数
为常数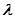 ,则
,则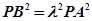
即
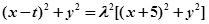 ……①,又
……①,又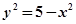 ……②
……②由①②可得
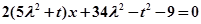 对任意
对任意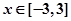 恒成立
恒成立所以
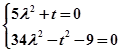 解得
解得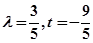 或
或 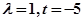 (舍去)
(舍去)所以存在点B
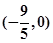 对于圆上任意一点P都有
对于圆上任意一点P都有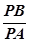 为常数
为常数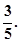

练习册系列答案
相关题目
 与圆
与圆 交于E、F两点,则
交于E、F两点,则 EOF(O为原点)的面积为
EOF(O为原点)的面积为



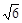
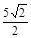
 和圆
和圆 相交于点A、B,则AB的垂直平分线方程是
相交于点A、B,则AB的垂直平分线方程是 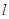 :
: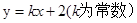 过椭圆
过椭圆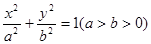 的上顶点B和左焦点F,且被圆
的上顶点B和左焦点F,且被圆 截得的弦长为
截得的弦长为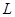 ,若
,若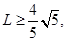 则椭圆离心率
则椭圆离心率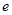 的取值范围是( )
的取值范围是( )




 上恰有两个点到直线
上恰有两个点到直线 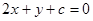 的距离等于1的
的距离等于1的 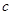 的一个可能值为( )
的一个可能值为( )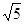
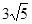
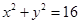 上的两点,且|AB|=6,若以AB为直径的圆M恰好经过
上的两点,且|AB|=6,若以AB为直径的圆M恰好经过 被圆
被圆 截得的弦长为4,
截得的弦长为4, 的最小值是 .
的最小值是 . 的点共( )
的点共( )