题目内容
若直线 被圆
被圆 截得的弦长为4,
截得的弦长为4,
则 的最小值是 .
的最小值是 .
 被圆
被圆 截得的弦长为4,
截得的弦长为4,则
 的最小值是 .
的最小值是 .9
解:由x2+y2+2x-4y+1=0得:(x+1)2+(y-2)2=4,
∴该圆的圆心为O(-1,2),半径r=2;
又直线2ax-by+2=0(a>0,b>0)被圆x2+y2+2x-4y+1=0截得的弦长为4,
∴直线2ax-by+2=0(a>0,b>0)经过圆心O(-1,2),
∴-2a-2b+2=0,即a+b=1,又a>0,b>0,
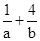 =
=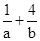 (a+b)=5+
(a+b)=5+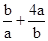
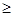 9
9
∴该圆的圆心为O(-1,2),半径r=2;
又直线2ax-by+2=0(a>0,b>0)被圆x2+y2+2x-4y+1=0截得的弦长为4,
∴直线2ax-by+2=0(a>0,b>0)经过圆心O(-1,2),
∴-2a-2b+2=0,即a+b=1,又a>0,b>0,
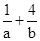 =
=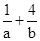 (a+b)=5+
(a+b)=5+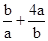
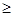 9
9
练习册系列答案
相关题目
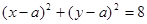 上总存在两个点到原点的距离为
上总存在两个点到原点的距离为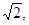 则实数
则实数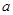 的取值范围是 .
的取值范围是 . 向圆C:
向圆C: 引切线,则切线长的最小值为( )
引切线,则切线长的最小值为( )
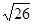

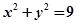 ,点A
,点A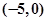 ,直线
,直线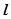 :
: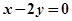
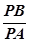 为常数,若存在,求出点B,不存在说明理由.
为常数,若存在,求出点B,不存在说明理由. (
( )被圆
)被圆 截得的弦长为
截得的弦长为 的最小值为( )
的最小值为( )

 与圆
与圆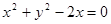 相切,则
相切,则 的值为 .
的值为 . 的参数方程是
的参数方程是 ,圆C的极坐标方程为
,圆C的极坐标方程为 .
. ,动点N在圆
,动点N在圆 上运动,线段MN的
上运动,线段MN的 与点P的轨迹相切,且
与点P的轨迹相切,且 轴.
轴. 轴上的截距相等,求直线
轴上的截距相等,求直线