题目内容
直线 和圆
和圆 相交于点A、B,则AB的垂直平分线方程是
相交于点A、B,则AB的垂直平分线方程是
 和圆
和圆 相交于点A、B,则AB的垂直平分线方程是
相交于点A、B,则AB的垂直平分线方程是 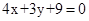
本试题主要是考查了直线与圆的位置关系的运用。
研究直线与圆的相交弦问题,那么联立方程组可知 和
和 ,得到关于x的一元二次方程
,得到关于x的一元二次方程
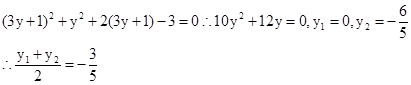 ,
,
那么结合韦达定理得到A(-1,0),B(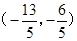 ,),因此可知AB的斜率为
,),因此可知AB的斜率为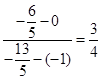 ,而其中垂线的斜率是其的负倒数,故垂直平分线的斜率为
,而其中垂线的斜率是其的负倒数,故垂直平分线的斜率为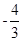 ,AB的中点为
,AB的中点为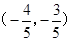 ,然后利用点斜式表示出方程为
,然后利用点斜式表示出方程为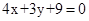 。
。
解决该试题的关键是利用直线与圆的方程联立方程组,结合韦达定理得到AB的中点坐标,利用直线的垂直关系得到AB的垂直平分线的斜率,得到方程。
研究直线与圆的相交弦问题,那么联立方程组可知
 和
和 ,得到关于x的一元二次方程
,得到关于x的一元二次方程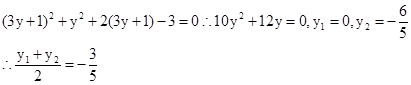 ,
,那么结合韦达定理得到A(-1,0),B(
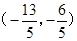 ,),因此可知AB的斜率为
,),因此可知AB的斜率为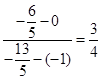 ,而其中垂线的斜率是其的负倒数,故垂直平分线的斜率为
,而其中垂线的斜率是其的负倒数,故垂直平分线的斜率为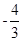 ,AB的中点为
,AB的中点为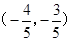 ,然后利用点斜式表示出方程为
,然后利用点斜式表示出方程为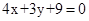 。
。解决该试题的关键是利用直线与圆的方程联立方程组,结合韦达定理得到AB的中点坐标,利用直线的垂直关系得到AB的垂直平分线的斜率,得到方程。

练习册系列答案
相关题目
 上的两点,且CF=CB,过C作CD^AF交AF的延长线与点D.
上的两点,且CF=CB,过C作CD^AF交AF的延长线与点D.
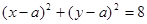 上总存在两个点到原点的距离为
上总存在两个点到原点的距离为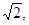 则实数
则实数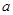 的取值范围是 .
的取值范围是 . 与圆
与圆 相切,则
相切,则 ,
, 满足的关系式为 .
满足的关系式为 .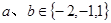 ,求直线
,求直线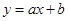 与圆
与圆 有公共点的概率为___________.
有公共点的概率为___________. 向圆C:
向圆C: 引切线,则切线长的最小值为( )
引切线,则切线长的最小值为( )
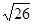

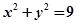 ,点A
,点A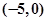 ,直线
,直线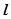 :
: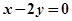
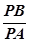 为常数,若存在,求出点B,不存在说明理由.
为常数,若存在,求出点B,不存在说明理由. ,动点N在圆
,动点N在圆 上运动,线段MN的
上运动,线段MN的 与点P的轨迹相切,且
与点P的轨迹相切,且 轴.
轴. 轴上的截距相等,求直线
轴上的截距相等,求直线