题目内容
已知直线l1：2x+ycosθ=0与直线l2：x（3+2cosθ）+y+2=0平行，其中θ是锐角三角形的一个内角，则θ的值为（ ）
分析：利用l1∥l2，且θ为锐角，可得斜率的关系-
=-(3+2cosθ)，解出即可．
| 2 |
| cosθ |
解答：解：∵l1∥l2，且θ为锐角，
∴-
=-(3+2cosθ)，化为2cos2θ+3cosθ-2=0，解得cosθ=
，
∴θ=60°．
故选A．
∴-
| 2 |
| cosθ |
| 1 |
| 2 |
∴θ=60°．
故选A．
点评：熟练掌握直线平行与斜率的关系是解题的关键．
练习册系列答案
相关题目
已知直线l1：2x-my+1=0与l2：x+（m-1）y-1=0，则“m=2”是“l1⊥l2”的（ ）
| A、充分不必要条件 | B、必要不充分条件 | C、充分且必要条件 | D、既不充分又不必要条件 |
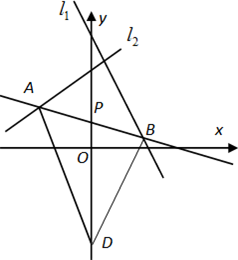如图，直线L过点P（0，1），夹在两已知直线l1：2x+y-8=0和l2：x-3y+10=0之间的线段AB恰被点P平分．