题目内容
已知直线l1:2x-y+3=0和直线l2:x+y-9=0
(1)求这两条直线的交点p;
(2)求经过点p和原点的直线方程;
(3)求经过点p且与直线l1垂直的直线方程.
(1)求这两条直线的交点p;
(2)求经过点p和原点的直线方程;
(3)求经过点p且与直线l1垂直的直线方程.
分析:(1)联立
解得即可;
(2)由于kOP=
,可得直线OP为:y=
x.
(3)由直线l1:2x-y+3=0,可得斜率kl1=2.可得与l1垂直的直线的斜率为-
.即可经过点p且与直线l1垂直的直线方程.
|
(2)由于kOP=
| 7 |
| 2 |
| 7 |
| 2 |
(3)由直线l1:2x-y+3=0,可得斜率kl1=2.可得与l1垂直的直线的斜率为-
| 1 |
| 2 |
解答:解:(1)联立
解得
,∴交点P(2,7)
(2)∵kOP=
,可得直线OP为:y=
x,即7x-2y=0.
(3)由直线l1:2x-y+3=0,可得斜率kl1=2.
∴与l1垂直的直线的斜率为-
.
因此经过点p且与直线l1垂直的直线方程为:y-7=-
(x-2).
化为x+2y-16=0.
|
|
(2)∵kOP=
| 7 |
| 2 |
| 7 |
| 2 |
(3)由直线l1:2x-y+3=0,可得斜率kl1=2.
∴与l1垂直的直线的斜率为-
| 1 |
| 2 |
因此经过点p且与直线l1垂直的直线方程为:y-7=-
| 1 |
| 2 |
化为x+2y-16=0.
点评:本题考查了直线的方程、相互垂直的直线斜率之间的关系,属于基础题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
已知直线l1:2x-my+1=0与l2:x+(m-1)y-1=0,则“m=2”是“l1⊥l2”的( )
| A、充分不必要条件 | B、必要不充分条件 | C、充分且必要条件 | D、既不充分又不必要条件 |
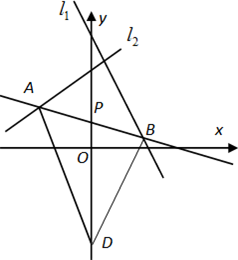 如图,直线L过点P(0,1),夹在两已知直线l1:2x+y-8=0和l2:x-3y+10=0之间的线段AB恰被点P平分.
如图,直线L过点P(0,1),夹在两已知直线l1:2x+y-8=0和l2:x-3y+10=0之间的线段AB恰被点P平分.