题目内容
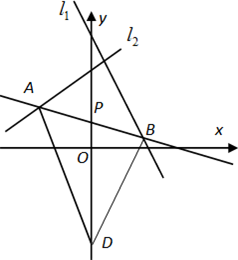 如图,直线L过点P(0,1),夹在两已知直线l1:2x+y-8=0和l2:x-3y+10=0之间的线段AB恰被点P平分.
如图,直线L过点P(0,1),夹在两已知直线l1:2x+y-8=0和l2:x-3y+10=0之间的线段AB恰被点P平分.(1)求直线l的方程;
(2)设点D(0,m),且AD∥l1,求:△ABD的面积.
分析:(1)设出直线l1上的动点B的坐标,由中点坐标公式求出A的坐标,代入直线l2的方程求得a的值;
(2)利用直线平行斜率相等求出m的值,得到D的坐标,由两点间的距离公式求出AD的长度,由点到直线的距离公式求出AD边上的高,代入面积公式得答案.
(2)利用直线平行斜率相等求出m的值,得到D的坐标,由两点间的距离公式求出AD的长度,由点到直线的距离公式求出AD边上的高,代入面积公式得答案.
解答:解:(1)∵点B在直线l1:2x+y-8=0上,可设B(a,8-2a),
又P(0,1)是AB的中点,
∴A(-a,2a-6),
∵点A在直线l2:x-3y+10=0上,∴-a-3(2a-6)+10=0,
解得a=4,即B(4,0).
故直线l的方程是x+4y-4=0;
(2)由(1)知A(-4,2),
又AD∥l1,则kAD=
=-2,
∴m=-6,则D(0,-6).
点A到直线l1的距离d=
=
,
|AD|=
=4
,
∴S△ABD=
|AD|•d=
•4
•
=28.
又P(0,1)是AB的中点,
∴A(-a,2a-6),
∵点A在直线l2:x-3y+10=0上,∴-a-3(2a-6)+10=0,
解得a=4,即B(4,0).
故直线l的方程是x+4y-4=0;
(2)由(1)知A(-4,2),
又AD∥l1,则kAD=
| 2-m |
| -4-0 |
∴m=-6,则D(0,-6).
点A到直线l1的距离d=
| |-4×2+2×1-8| | ||
|
14
| ||
| 5 |
|AD|=
| (-4-0)2+(2+6)2 |
| 5 |
∴S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 14 | ||
|
点评:本题考查了点到直线的距离公式,考查了两条直线的交点问题,训练了直线平行和斜率的关系.

练习册系列答案
相关题目
 如图,P是抛物线C:y=
如图,P是抛物线C:y= 如图,P是抛物线C:x2=2y上一点,F为抛物线的焦点,直线l过点P且与抛物线交于另一点Q,已知P(x1,y1),Q(x2,y2).
如图,P是抛物线C:x2=2y上一点,F为抛物线的焦点,直线l过点P且与抛物线交于另一点Q,已知P(x1,y1),Q(x2,y2). 如图,直线l过点P(4,1),交x轴、y轴正半轴于A、B两点;
如图,直线l过点P(4,1),交x轴、y轴正半轴于A、B两点; 如图所示,过点P (0,-2)的直线l交抛物线y2=4x于A,B两点,求以OA,OB为邻边的平行四边形OAMB的顶点M的轨迹方程.
如图所示,过点P (0,-2)的直线l交抛物线y2=4x于A,B两点,求以OA,OB为邻边的平行四边形OAMB的顶点M的轨迹方程.