题目内容
【题目】如图，在四棱锥P－ABCD中，平面PAD⊥平面ABCD，AB＝AD，∠BAD＝60°，E，F分别是AP，AD的中点．
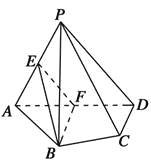
求证：（1）直线EF∥平面PCD；
（2）平面BEF⊥平面PAD．
【答案】（1）详见解析（2）详见解析
【解析】试题分析：（1）要证直线EF∥平面PCD，只需证明EF∥PD，EF不在平面PCD中，PD平面PCD即可；（2）连接BD，证明BF⊥AD．说明平面PAD∩平面ABCD=AD，推出BF⊥平面PAD；然后证明平面BEF⊥平面PAD
试题解析：（1）在△PAD中，因为E，F分别为AP，AD的中点，所以EF∥PD．
又因为EF不在平面PCD中，PD?平面PCD
所以直线EF∥平面PCD．
（2）连接BD．因为AB=AD，∠BAD=60°．
所以△ABD为正三角形．因为F是AD的中点，所以BF⊥AD．
因为平面PAD⊥平面ABCD，BF?平面ABCD，
平面PAD∩平面ABCD=AD，所以BF⊥平面PAD．
又因为BF平面EBF，所以平面BEF⊥平面PAD
练习册系列答案
相关题目
【题目】我国的高铁技术发展迅速，铁道部门计划在
两城市之间开通高速列车，假设列车在试运行期间，每天在
两个时间段内各发一趟由
城开往
城的列车（两车发车情况互不影响），
城发车时间及概率如下表所示：
发车 时间 |
|
|
|
|
|
|
概率 |
|
|
|
|
|
|
若甲、乙两位旅客打算从城到
城，他们到达
火车站的时间分别是周六的
和周日的
（只考虑候车时间，不考虑其他因素）．
（1）设乙候车所需时间为随机变量
（单位：分钟），求
的分布列和数学期望
；
（2）求甲、乙两人候车时间相等的概率．
