Question

【题目】已知函数， .

（Ⅰ）当时，求函数切线斜率中的最大值；

（Ⅱ）若关于的方程有解，求实数的取值范围.

Answer 1

【答案】（Ⅰ）1;（Ⅱ）或.

【解析】试题分析：（Ⅰ）根据导数的几何意义，切线斜率的最大值即的最大值，对函数进行求导，通过配方法可求其最大值；（Ⅱ）令，则问题等价于函数存在零点，根据函数的单调性解出即可；

试题解析：（Ⅰ）函数的定义域为.

当时， ，

所以函数切线斜率的最大值为1.

（Ⅱ）因为关于的方程有解，

令，则问题等价于函数存在零点，

所以.

当时， 对成立，

函数在上单调递减.

而， ，

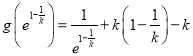
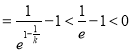所以函数存在零点.

当时，令，得.

， 随的变化情况如下表：

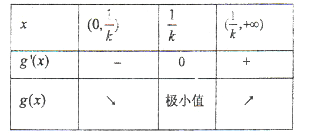
所以为函数的最小值，

当时，即时，函数没有零点，

当时，即时，注意到，

所以函数存在零点.

综上，当或时，关于的方程有解.