题目内容
已知f(x)是可导的函数,且f′(x)<f(x)对于x∈R恒成立,则( )A.f(1)<ef(0),f(2013)>e2013f(0)
B.f(1)>ef(0),f(2013)>e2013f(0)
C.f(1)>ef(0),f(2013)<e2013f(0)
D.f(1)<ef(0),f(2013)<e2013f(0)
【答案】分析:构造函数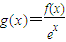 ,利用导数判断其单调性即可得出.
,利用导数判断其单调性即可得出.
解答:解:令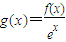 ,则
,则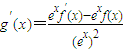 =
=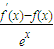 <0.
<0.
∴函数g(x)在R上单调递减.
∴g(1)<g(0),g(2013)<g(0).
即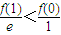 ,
,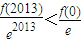 ,
,
化为f(1)<ef(0),f(2013)<e2013f(0).
故选D.
点评:本题是一个知识点交汇的综合题,考查综合运用函数思想解题的能力.恰当构造函数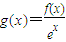 ,利用导数判断其单调性是解题的关键.
,利用导数判断其单调性是解题的关键.
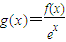 ,利用导数判断其单调性即可得出.
,利用导数判断其单调性即可得出.解答:解:令
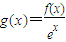 ,则
,则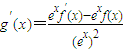 =
=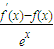 <0.
<0.∴函数g(x)在R上单调递减.
∴g(1)<g(0),g(2013)<g(0).
即
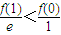 ,
,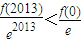 ,
,化为f(1)<ef(0),f(2013)<e2013f(0).
故选D.
点评:本题是一个知识点交汇的综合题,考查综合运用函数思想解题的能力.恰当构造函数
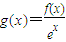 ,利用导数判断其单调性是解题的关键.
,利用导数判断其单调性是解题的关键. 
练习册系列答案
相关题目