题目内容
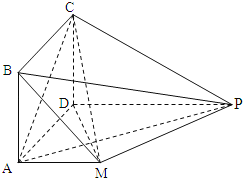
【题目】已知抛物线的焦点为F,过抛物线上一点P作抛物线的切线交x轴于点D,交y轴于Q点,当时,.
(1)判断的形状,并求抛物线的方程;
(2)若两点在抛物线上,且满足![]() ,其中点,若抛物线上存在异于
,其中点,若抛物线上存在异于![]() 的点H,使得经过
的点H,使得经过![]() 三点的圆和抛物线在点处有相同的切线,求点H的坐标.
三点的圆和抛物线在点处有相同的切线,求点H的坐标.
【答案】(Ⅰ)等腰三角形,见解析(Ⅱ)![]()
【解析】
试题(1)设P(x1,y1),求出切线l的方程,求解三角形的顶点坐标,排除边长关系,然后判断三角形的形状,然后求解抛物线方程.
(2)求出A,B的坐标分别为(0,0),(4,4),设H(x0,y0)(x0≠0,x0≠4),求出AB的中垂线方程,AH的中垂线方程,解得圆心坐标,由![]() ,求解H点坐标即可.
,求解H点坐标即可.
试题解析:
(1) (1)设P(x1,y1),
则切线l的方程为![]() ,且
,且![]() ,
,
所以![]() ,
,![]() ,所以|FQ|=|FP|,
,所以|FQ|=|FP|,
所以△PFQ为等腰三角形,且D为PQ的中点,
所以DF⊥PQ,因为|DF|=2,∠PFD=60°,
所以∠QFD=60°,所以![]() ,得p=2,
,得p=2,
所以抛物线方程为x2=4y;
(2)由已知,得A,B的坐标分别为(0,0),(4,4),
设H(x0,y0)(x0≠0,x0≠4),
AB的中垂线方程为y=﹣x+4,①AH的中垂线方程为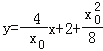 ,②
,②
联立①②,解得圆心坐标为:![]() ,
,
kNH=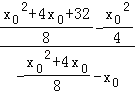 =
=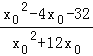 ,
,
由![]() ,得
,得![]() ,
,
因为x0≠0,x0≠4,所以x0=﹣2,
所以H点坐标为(﹣2,1).

练习册系列答案
相关题目