题目内容
【题目】已知函数![]() 是定义在
是定义在![]() 上的奇函数,在
上的奇函数,在![]() 上是增函数,且
上是增函数,且![]() ,给出下列结论,
,给出下列结论,
①若![]() 且
且![]() ,则
,则![]() ;
;
②若![]() 且
且![]() ,则
,则![]() ;
;
③若方程![]() 在
在![]() 内恰有四个不同的实根
内恰有四个不同的实根![]() ,
, ![]() ,
, ![]() ,
, ![]() ,则
,则![]() 或8;
或8;
④函数![]() 在
在![]() 内至少有5个零点,至多有13个零点.
内至少有5个零点,至多有13个零点.
其中结论正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】试题分析:∵![]() 是奇函数且
是奇函数且![]() ,∴
,∴![]() ∴函数
∴函数![]() 为周期
为周期![]() 的周期函数,根据题意可画出这样的图形:如图所示,
的周期函数,根据题意可画出这样的图形:如图所示,
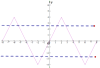
∵定义在![]() 上的奇函数,在
上的奇函数,在![]() 上是增函数,∴在
上是增函数,∴在![]() 上是增函数,即
上是增函数,即![]() 上是增函数,①若
上是增函数,①若![]() 且
且![]() ,则
,则![]() ,∴
,∴![]() ,又∵
,又∵![]() ,∴
,∴![]() ,即
,即![]() ,故①正确;②若
,故①正确;②若![]() 且
且![]() ,则
,则![]() ,观察可知
,观察可知![]() ,故②正确;③若方程
,故②正确;③若方程![]() 在
在![]() 内恰有四个不同的实根
内恰有四个不同的实根![]() ,当
,当![]() 时(如上方虚线所示),可知,左边两个交点之和为
时(如上方虚线所示),可知,左边两个交点之和为![]() (因为两个交点关于
(因为两个交点关于![]() 对称,一个交点可表示为
对称,一个交点可表示为![]() ,另一个交点可表示为
,另一个交点可表示为![]() )。
)。![]() 轴右边的两个交点之和为
轴右边的两个交点之和为![]() ,则
,则![]() ,同理
,同理![]() 时
时![]() ,故③正确;④函数
,故③正确;④函数![]() 在
在![]() 内有
内有![]() 个零点,故④不正确,结论正确的有①②③,故选:C。
个零点,故④不正确,结论正确的有①②③,故选:C。

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目