题目内容
某海域有 、
、 两个岛屿,
两个岛屿, 岛在
岛在 岛正东4海里处。经多年观察研究发现,某种鱼群洄游的路线是曲线
岛正东4海里处。经多年观察研究发现,某种鱼群洄游的路线是曲线 ,曾有渔船在距
,曾有渔船在距 岛、
岛、 岛距离和为8海里处发现过鱼群。以
岛距离和为8海里处发现过鱼群。以 、
、 所在直线为
所在直线为 轴,
轴, 的垂直平分线为
的垂直平分线为 轴建立平面直角坐标系。
轴建立平面直角坐标系。
(1)求曲线 的标准方程;(6分)
的标准方程;(6分)
(2)某日,研究人员在 、
、 两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同),
两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同), 、
、 两岛收到鱼群在
两岛收到鱼群在 处反射信号的时间比为
处反射信号的时间比为 ,问你能否确定
,问你能否确定 处的位置(即点
处的位置(即点 的坐标)?(8分)
的坐标)?(8分)
(1)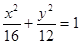 ;(2)点
;(2)点 的坐标为
的坐标为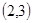 或
或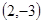 。
。
解析试题分析:(1)由题意知曲线 是以
是以 、
、 为焦点且长轴长为8的椭圆 3分
为焦点且长轴长为8的椭圆 3分
又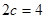 ,则
,则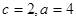 ,故
,故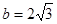 5分
5分
所以曲线 的方程是
的方程是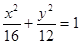 6分
6分
(2)由于 、
、 两岛收到鱼群发射信号的时间比为
两岛收到鱼群发射信号的时间比为 ,
,
因此设此时距 、
、 两岛的距离分别比为
两岛的距离分别比为 7分
7分
即鱼群分别距 、
、 两岛的距离为5海里和3海里。 8分
两岛的距离为5海里和3海里。 8分
设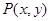 ,
,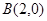 ,由
,由
 , 10分
, 10分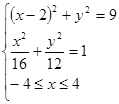 , 12分
, 12分 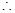
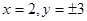 13分
13分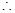 点
点 的坐标为
的坐标为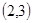 或
或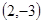 14分
14分
考点:本题主要考查椭圆的定义、标准方程,椭圆与圆的位置关系。
点评:中档题,利用椭圆的定义,明确曲线是椭圆并求得其标准方程为,作为实际问题解决,很好的体现了数学的妙用。

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 与双曲线
与双曲线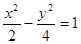 有共同的渐近线,且经过点
有共同的渐近线,且经过点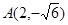 ,椭圆
,椭圆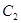 以双曲线
以双曲线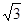 ,求双曲线
,求双曲线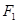
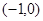 、
、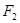
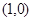 为椭圆的焦点,且直线
为椭圆的焦点,且直线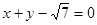 与椭圆相切.
与椭圆相切. 、
、 两点,求△
两点,求△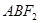 的面积
的面积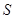 的最大值,并求此时直线的方程。
的最大值,并求此时直线的方程。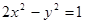 的右支交于不同的两点A,B.
的右支交于不同的两点A,B.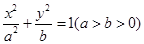 的左、右焦点分别为
的左、右焦点分别为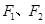 ,离心率
,离心率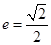 ,
, 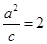 .
. 的直线
的直线 与该椭圆交于
与该椭圆交于 两点,且
两点,且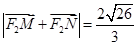 ,求直线
,求直线 中,已知椭圆
中,已知椭圆 ,经过点
,经过点 ,其中e为椭圆的离心率.且椭圆
,其中e为椭圆的离心率.且椭圆 与直线
与直线 有且只有一个交点。
有且只有一个交点。
 与椭圆
与椭圆 在椭圆上,直线
在椭圆上,直线 平分线段
平分线段 ,求:当
,求:当 的面积取得最大值时直线
的面积取得最大值时直线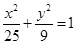 有相同的焦点,求此双曲线方程.
有相同的焦点,求此双曲线方程. 过点
过点 ,且离心率e=
,且离心率e=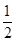 .
. 与椭圆交于不同的两点
与椭圆交于不同的两点 、
、 ,且线段
,且线段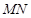 的垂直平分线过定点
的垂直平分线过定点 ,求
,求 的取值范围。
的取值范围。 与
与 轴相切,圆心
轴相切,圆心 上且在第二象限,直线
上且在第二象限,直线 过点
过点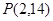 .
. 的方程;
的方程; 两点且
两点且 ,求直线
,求直线