题目内容
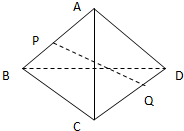 如图,正四面体ABCD各棱长均为1,P,Q分别在棱AB,CD上,且
如图,正四面体ABCD各棱长均为1,P,Q分别在棱AB,CD上,且| 1 |
| 3 |
| 2 |
| 3 |
[
,2]
| 1 |
| 2 |
[
,2]
.| 1 |
| 2 |
分析:作PE∥AC,连接EQ,由题意,EQ∥BD,PE⊥EQ,则∠PQE为直线PQ与直线BD所成角,再考虑两个极端位置,即可求得结论.
解答: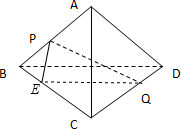 解:作PE∥AC,连接EQ,由题意,EQ∥BD,PE⊥EQ,则∠PQE为直线PQ与直线BD所成角
解:作PE∥AC,连接EQ,由题意,EQ∥BD,PE⊥EQ,则∠PQE为直线PQ与直线BD所成角
①AP=CQ=
时,PE=
AC,EQ=
AC,∴tan∠PQE=
=2;
②AP=CQ=
时,PE=
AC,EQ=
AC,∴tan∠PQE=
=
,
∴直线PQ与直线BD所成角的正切值的取值范围是[
,2]
故答案为:[
,2]
 解:作PE∥AC,连接EQ,由题意,EQ∥BD,PE⊥EQ,则∠PQE为直线PQ与直线BD所成角
解:作PE∥AC,连接EQ,由题意,EQ∥BD,PE⊥EQ,则∠PQE为直线PQ与直线BD所成角①AP=CQ=
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| PE |
| EQ |
②AP=CQ=
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| PE |
| EQ |
| 1 |
| 2 |
∴直线PQ与直线BD所成角的正切值的取值范围是[
| 1 |
| 2 |
故答案为:[
| 1 |
| 2 |
点评:本题考查线线角,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案
相关题目
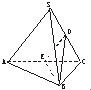 如图,正四面体S-ABC中,D为SC的中点,则BD与SA所成角的余弦值是( )
如图,正四面体S-ABC中,D为SC的中点,则BD与SA所成角的余弦值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 9、如图,正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线Ox,Oy,Oz上,则在下列命题中,错误的为( )
9、如图,正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线Ox,Oy,Oz上,则在下列命题中,错误的为( ) 14、如图,正四面体ABCD的顶点A、B、C分别在两两垂直的三条射线Ox、Oy、Oz上,给出下列四个命题:
14、如图,正四面体ABCD的顶点A、B、C分别在两两垂直的三条射线Ox、Oy、Oz上,给出下列四个命题: 如图:正四面体S-ABC中,如果E,F分别是SC,AB的中点,那么异面直线EF与SA所成的角等于( )
如图:正四面体S-ABC中,如果E,F分别是SC,AB的中点,那么异面直线EF与SA所成的角等于( ) 如图,正四面体S-ABC的边长为a,D是SA的中点,E是BC的中点,则SDE绕SE旋转一周所得旋转体的体积为
如图,正四面体S-ABC的边长为a,D是SA的中点,E是BC的中点,则SDE绕SE旋转一周所得旋转体的体积为