题目内容
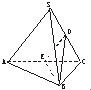 如图,正四面体S-ABC中,D为SC的中点,则BD与SA所成角的余弦值是( )
如图,正四面体S-ABC中,D为SC的中点,则BD与SA所成角的余弦值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:观察图象发现,取AC的中点E,连接DE,BE,则可证得∠BDE就是BD与SA所成的角,在三角形BDE中求解即可.
解答: 解:如图取AC的中点E,连接DE、BE,则DE∥SA,
解:如图取AC的中点E,连接DE、BE,则DE∥SA,
∴∠BDE就是BD与SA所成的角.
设SA=a,则BD=BE=
a,DE=
a,
cos∠BDE=
=
.
故选C
 解:如图取AC的中点E,连接DE、BE,则DE∥SA,
解:如图取AC的中点E,连接DE、BE,则DE∥SA,∴∠BDE就是BD与SA所成的角.
设SA=a,则BD=BE=
| ||
| 2 |
| 1 |
| 2 |
cos∠BDE=
| BD2+DE2-BE2 |
| 2BD•DE |
| ||
| 6 |
故选C
点评:本题考查异面直线所成的角的余弦值的求法,其步骤是作角,证角,求角,本类题中有一个易错点,由于两个直线所成的角是大于等于00,小于等于900,而所求得的余弦值可能为负,若此种情况出现,则说明求得是两线所成角的补角,补角的补角即为所求.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 如图:正四面体S-ABC中,如果E,F分别是SC,AB的中点,那么异面直线EF与SA所成的角等于( )
如图:正四面体S-ABC中,如果E,F分别是SC,AB的中点,那么异面直线EF与SA所成的角等于( ) 如图,正四面体S-ABC的边长为a,D是SA的中点,E是BC的中点,则SDE绕SE旋转一周所得旋转体的体积为
如图,正四面体S-ABC的边长为a,D是SA的中点,E是BC的中点,则SDE绕SE旋转一周所得旋转体的体积为








