题目内容
 如图,正四面体S-ABC的边长为a,D是SA的中点,E是BC的中点,则SDE绕SE旋转一周所得旋转体的体积为
如图,正四面体S-ABC的边长为a,D是SA的中点,E是BC的中点,则SDE绕SE旋转一周所得旋转体的体积为
| ||
| 36 |
| ||
| 36 |
分析:连接AE,先证ED⊥SA,作DF⊥SE,交SE于点F,从而可知所求的旋转体的体积是以DF为底面半径,分别以SF和EF为高的两个圆锥的体积的和,然后求出DF,SE,即可求出所求.
解答:解:连接AE,因为△SDE和△ABC都是边长为a的正三角形,并且SE和AE分别是它们的中线,
所以SE=AE,从而△SDE为等腰三角形,由于D是SA的中点,
所以ED⊥SA.作DF⊥SE,交SE于点F.考虑直角△SDE的面积,得到
SE•DF=
SD•DE,所以,DF=
=
.易知,SE=
=
=
a,
DE=
=
=
a,所以,DF=
•
=
a.
所求的旋转体的体积是以DF为底面半径,分别以SF和EF为高的两个圆锥的体积的和,即
π•(
a)2•SF+
π•(
a)2•EF=
π•(
a)2•SE=
π•
•
a=
πa3.
故答案为:
πa3.
所以SE=AE,从而△SDE为等腰三角形,由于D是SA的中点,
所以ED⊥SA.作DF⊥SE,交SE于点F.考虑直角△SDE的面积,得到
| 1 |
| 2 |
| 1 |
| 2 |
| SD•DE |
| SE |
| ||
| SE |
| SB2-BE2 |
a2-(
|
| ||
| 2 |
DE=
| SE2-SD2 |
|
| ||
| 2 |
| a |
| 2 |
| ||||
|
| ||
| 6 |
所求的旋转体的体积是以DF为底面半径,分别以SF和EF为高的两个圆锥的体积的和,即
| 1 |
| 3 |
| ||
| 6 |
| 1 |
| 3 |
| ||
| 6 |
| 1 |
| 3 |
| ||
| 6 |
| 1 |
| 3 |
| a2 |
| 6 |
| ||
| 2 |
| ||
| 36 |
故答案为:
| ||
| 36 |
点评:本题主要考查了旋转题的体积,解题的关键是弄清旋转体的形状,本题旋转体是以DF为底面半径,分别以SF和EF为高的两个圆锥,属于中档题.

练习册系列答案
相关题目
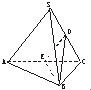 如图,正四面体S-ABC中,D为SC的中点,则BD与SA所成角的余弦值是( )
如图,正四面体S-ABC中,D为SC的中点,则BD与SA所成角的余弦值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图:正四面体S-ABC中,如果E,F分别是SC,AB的中点,那么异面直线EF与SA所成的角等于( )
如图:正四面体S-ABC中,如果E,F分别是SC,AB的中点,那么异面直线EF与SA所成的角等于( )








