题目内容
【题目】一个几何体的三视图及尺寸如图所示，则该几何体的外接球半径为（ ）
A.
B.
C.
D.
【答案】C
【解析】解：由三视图可知：该几何体是一个如图所示的三棱锥（图中红色部分），它是一个正四棱锥的一半，
其中底面是一个两直角边都为6的直角三角形，高EF=4．
设其外接球的球心为O，O点必在高线EF上，外接球半径为R，
则在直角三角形AOF中，AO2=OF2+AF2=（EF﹣EO）2+AF2 ，
即R2=（4﹣R）2+（3 
）2 ，
解得：R= 
故选C．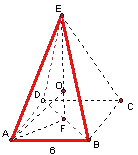
由三视图可知：该几何体是一个如图所示的三棱锥（图中红色部分），它是一个正四棱锥的一半，其中底面是一个两直角边都为6的直角三角形，高为4．设其外接球的球心O必在高线EF上，利用外接球的半径建立方程，据此方程可求出答案．
练习册系列答案
金钥匙试卷系列答案
相关题目
【题目】某市举办校园足球赛，组委会为了做好服务工作，招募了12名男志愿者和10名女志愿者，调查发现男女志愿者中分别有8人和4人喜欢看足球比赛，其余不喜欢
（1）根据以上数据完成以下2×2列联表：
喜欢看足球比赛 | 不喜欢看足球比赛 | 总计 | |
男 | |||
女 | |||
总计 |
（2）根据列联表的独立性检验，能否在犯错误的概率不超过0.10的前提下认为性别与喜欢看足球比赛有关？
（3）从女志愿者中抽取2人参加某场足球比赛服务工作，若其中喜欢看足球比赛的人数为ξ，求ξ的分布列和数学期望．
附：参考公式：K2= 
，其中n=a+b+c+d
参考数据：
P（K2≥k0） | 0.4 | 0.25 | 0.10 | 0.010 |
k0 | 0.708 | 1.323 | 2.706 | 6.635 |
