题目内容
在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系.圆C1,直线C2的极坐标方程分别为ρ=4sin θ,ρcos 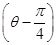 =2
=2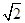 .
.
(1)求C1与C2交点的极坐标;
(2)设P为C1的圆心,Q为C1与C2交点连线的中点.已知直线PQ的参数方程为 (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值.
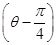 =2
=2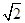 .
.(1)求C1与C2交点的极坐标;
(2)设P为C1的圆心,Q为C1与C2交点连线的中点.已知直线PQ的参数方程为
 (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值.(1) ,
,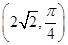 (2)
(2)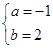
 ,
,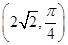 (2)
(2)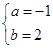
(1)圆C1的直角坐标方程为x2+(y-2)2=4,直线C2的直角坐标方程为x+y-4=0.
解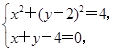 得
得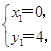 ,
,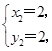
所以C1与C2交点的极坐标为 ,
,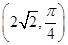 .
.
注:极坐标系下点的表示不唯一.
(2)由(1)可得,P点与Q点的直角坐标分别为(0,2),(1,3).
故直线PQ的直角坐标方程为x-y+2=0,
由参数方程可得y=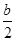 x-
x-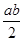 +1.
+1.
所以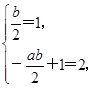 解得
解得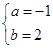
解
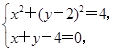 得
得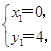 ,
,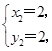
所以C1与C2交点的极坐标为
 ,
,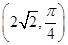 .
.注:极坐标系下点的表示不唯一.
(2)由(1)可得,P点与Q点的直角坐标分别为(0,2),(1,3).
故直线PQ的直角坐标方程为x-y+2=0,
由参数方程可得y=
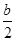 x-
x-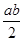 +1.
+1.所以
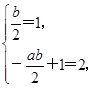 解得
解得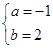

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
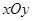 中,曲线
中,曲线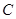 的参数方程为
的参数方程为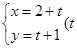 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点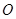 为极点,
为极点,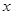 轴的正半轴为极轴的极坐标系下,曲线
轴的正半轴为极轴的极坐标系下,曲线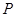 的方程为
的方程为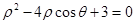 .
.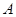 、
、 ,求
,求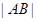 .
. (t为参数)相交于A、B两点,求|AB|.
(t为参数)相交于A、B两点,求|AB|.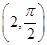 且与极轴平行的直线方程是( )
且与极轴平行的直线方程是( )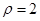
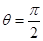
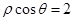
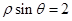
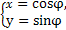 (φ为参数),曲线C2的参数方程为
(φ为参数),曲线C2的参数方程为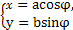 (a>b>0,φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α与C1,C2各有一个交点.当α=0时,这两个交点间的距离为2,当α=
(a>b>0,φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α与C1,C2各有一个交点.当α=0时,这两个交点间的距离为2,当α=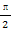 时,这两个交点重合.
时,这两个交点重合.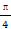 时,l与C1,C2的交点分别为A1,B1,当α=-
时,l与C1,C2的交点分别为A1,B1,当α=-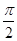 (ρ∈R)和ρcos θ=2
(ρ∈R)和ρcos θ=2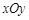 中,以原点
中,以原点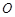 为极点,
为极点,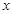 轴的正半轴为极轴建立极坐标系.若曲线
轴的正半轴为极轴建立极坐标系.若曲线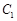 的参数方程为
的参数方程为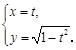 (
(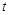 为参数),曲线
为参数),曲线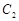 的极坐标方程为
的极坐标方程为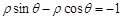 .则曲线
.则曲线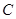 的极坐标方程为:
的极坐标方程为: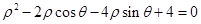 ,曲线C上的任意一个点P的直角坐标为
,曲线C上的任意一个点P的直角坐标为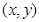 ,则
,则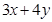 的取值范围为 .
的取值范围为 .