题目内容
14.已知数列{an}各项均为正数,首项a1=1,且其前n项和Sn满足Sn$\sqrt{{S}_{n-1}}$-Sn-1$\sqrt{{S}_{n}}$=2$\sqrt{{S}_{n}{S}_{n-1}}$(n∈N*且n≥2),则a21=( )| A. | 120 | B. | 160 | C. | 200 | D. | 240 |
分析 通过将Sn$\sqrt{{S}_{n-1}}$-Sn-1$\sqrt{{S}_{n}}$=2$\sqrt{{S}_{n}{S}_{n-1}}$(n∈N*且n≥2)两边同除以$\sqrt{{S}_{n}}$•$\sqrt{{S}_{n-1}}$可知$\sqrt{{S}_{n}}$-$\sqrt{{S}_{n-1}}$=2,进而可知数列{$\sqrt{{S}_{n}}$}是以1为首项、2为公差的等差数列,利用an=Sn-Sn-1计算即得结论.
解答 解:∵Sn$\sqrt{{S}_{n-1}}$-Sn-1$\sqrt{{S}_{n}}$=2$\sqrt{{S}_{n}{S}_{n-1}}$(n∈N*且n≥2),an>0,
∴$\frac{{S}_{n}\sqrt{{S}_{n-1}}-{S}_{n-1}\sqrt{{S}_{n}}}{\sqrt{{S}_{n-1}}\sqrt{{S}_{n}}}$=$\frac{2\sqrt{{S}_{n-1}{S}_{n}}}{\sqrt{{S}_{n-1}\sqrt{{S}_{n}}}}$,
即$\sqrt{{S}_{n}}$-$\sqrt{{S}_{n-1}}$=2,
又∵$\sqrt{{S}_{1}}$=$\sqrt{{a}_{1}}$=1,
∴$\sqrt{{S}_{n}}$=1+2(n-1)=2n-1,
∴Sn=(2n-1)2=4n2-4n+1,
∴an=Sn-Sn-1
=(4n2-4n+1)-[4(n-1)2-4(n-1)+1]
=8n-8(n≥2),
∴a21=21•8-8=160,
故选:B.
点评 本题考查数列的通项,注意解题方法的积累,属于中档题.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
6.已知数列{an}满足a1=0,an+1=$\frac{{{a_n}-2}}{{\frac{5}{4}{a_n}-2}}$,则a2015=( )
| A. | 0 | B. | 1 | C. | $\frac{4}{3}$ | D. | 2 |
9.下列四个函数中,在区间(0,$\frac{1}{4}$)上为减函数的是( )
| A. | y=x($\frac{1}{2}$)x | B. | y=-($\frac{1}{2}$)x | C. | y=xlog2x | D. | y=x${\;}^{\frac{1}{3}}$ |
19.同时投掷两颗骰子,则两颗骰子向上的点数相同的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
 是定义在实数集
是定义在实数集 上的奇函数,且当
上的奇函数,且当 时,
时, 成立,若
成立,若 ,则
,则 大小关系( )
大小关系( ) B.
B.
 D.
D.
 ,若当
,若当 时,不等式
时,不等式 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( ) B.
B.
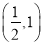 D.
D.