ЬтФПФкШн
ЁОЬтФПЁПвбжЊЕШБШЪ§Са{an}ЕФЙЋБШЮЊqЃЌМЧbn=amЃЈnЉ1ЃЉ+1+amЃЈnЉ1ЃЉ+2+Ё+amЃЈnЉ1ЃЉ+m ЃЌ cn=amЃЈnЉ1ЃЉ+1amЃЈnЉ1ЃЉ+2ЁamЃЈnЉ1ЃЉ+m ЃЌ ЃЈmЃЌnЁЪN*ЃЉЃЌдђвдЯТНсТлвЛЖЈе§ШЗЕФЪЧЃЈ ЃЉ
A.Ъ§Са{bn}ЮЊЕШВюЪ§СаЃЌЙЋВюЮЊqm
B.Ъ§Са{bn}ЮЊЕШБШЪ§СаЃЌЙЋБШЮЊq2m
C.Ъ§Са{cn}ЮЊЕШБШЪ§СаЃЌЙЋБШЮЊ ![]()
D.Ъ§Са{cn}ЮЊЕШБШЪ§СаЃЌЙЋБШЮЊ ![]()
ЁОД№АИЁПC
ЁОНтЮіЁПНтЃКЂй ![]() ЃЌЕБq=1ЪБЃЌbn=mamЃЈnЉ1ЃЉ ЃЌ bn+1=mamЃЈnЉ1ЃЉ+m=mamЃЈnЉ1ЃЉ=bn ЃЌ ДЫЪБЪЧГЃЪ§СаЃЌбЁЯюAВЛе§ШЗЃЌбЁЯюBе§ШЗЃЛ
ЃЌЕБq=1ЪБЃЌbn=mamЃЈnЉ1ЃЉ ЃЌ bn+1=mamЃЈnЉ1ЃЉ+m=mamЃЈnЉ1ЃЉ=bn ЃЌ ДЫЪБЪЧГЃЪ§СаЃЌбЁЯюAВЛе§ШЗЃЌбЁЯюBе§ШЗЃЛ
ЕБqЁй1ЪБЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌДЫЪБ
ЃЌДЫЪБ ![]() ЃЌбЁЯюBВЛе§ШЗЃЌ
ЃЌбЁЯюBВЛе§ШЗЃЌ
гжbn+1Љbn= ![]() ЃЌВЛЪЧГЃЪ§ЃЌЙЪбЁЯюAВЛе§ШЗЃЌ
ЃЌВЛЪЧГЃЪ§ЃЌЙЪбЁЯюAВЛе§ШЗЃЌ
ЂкЁпЕШБШЪ§Са{an}ЕФЙЋБШЮЊqЃЌЁр ![]() ЃЌ
ЃЌ
Ёр ![]() =
= ![]() ЃЌ
ЃЌ
Ёр ![]() =
= 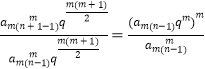 =
= ![]() ЃЌЙЪCе§ШЗDВЛе§ШЗЃЎ
ЃЌЙЪCе§ШЗDВЛе§ШЗЃЎ
злЩЯПЩжЊЃКжЛгаCе§ШЗЃЎ
ЙЪбЁCЃЎ
ЁОПМЕуОЋЮіЁПИљОнЬтФПЕФвбжЊЬѕМўЃЌРћгУЕШВюЙиЯЕЕФШЗЖЈКЭЕШБШЙиЯЕЕФШЗЖЈЕФЯрЙижЊЪЖПЩвдЕУЕНЮЪЬтЕФД№АИЃЌашвЊеЦЮеШчЙћвЛИіЪ§СаДгЕк2ЯюЦ№ЃЌУПвЛЯюгыЫќЕФЧАвЛЯюЕФВюЕШгкЭЌвЛИіГЃЪ§ЃЌМД![]() Ѓ
Ѓ![]() =d ЃЌЃЈnЁн2ЃЌnЁЪN
=d ЃЌЃЈnЁн2ЃЌnЁЪN![]() ЃЉФЧУДетИіЪ§СаОЭНазіЕШВюЪ§СаЃЛЕШБШЪ§СаПЩвдЭЈЙ§ЖЈвхЗЈЁЂжаЯюЗЈЁЂЭЈЯюЙЋЪНЗЈЁЂЧАnЯюКЭЗЈНјааХаЖЯЃЎ
ЃЉФЧУДетИіЪ§СаОЭНазіЕШВюЪ§СаЃЛЕШБШЪ§СаПЩвдЭЈЙ§ЖЈвхЗЈЁЂжаЯюЗЈЁЂЭЈЯюЙЋЪНЗЈЁЂЧАnЯюКЭЗЈНјааХаЖЯЃЎ

 ГЌФмбЇЕфгІгУЬтЬтПЈЯЕСаД№АИ
ГЌФмбЇЕфгІгУЬтЬтПЈЯЕСаД№АИЁОЬтФПЁПдкФГДЮВтЪджаЃЌОэУцТњЗжЮЊ100ЗжЃЌПМЩњЕУЗжЮЊећЪ§ЃЌЙцЖЈ60ЗжМАвдЩЯЮЊМАИё.ФГЕїбаПЮЬтаЁзщЮЊСЫЕїВщЮчанЖдПМЩњИДЯАаЇЙћЕФгАЯьЃЌЖдЮчанКЭВЛЮчанЕФПМЩњНјааСЫВтЪдГЩМЈЕФЭГМЦЃЌЪ§ОнШчЯТБэЃК

ЃЈ1ЃЉИљОнЩЯЪіБэИёЭъГЩЯТСаСаСЊБэЃК

ЃЈ2ЃЉХаЖЯЁАФмЗёдкЗИДэЮѓЕФИХТЪВЛГЌЙ§0.010ЕФЧАЬсЯТШЯЮЊГЩМЈМАИёгыЮчангаЙиЁБЃП
ЃЈВЮПМЙЋЪНЃК![]() ЃЌЦфжа
ЃЌЦфжа![]() .ЃЉ
.ЃЉ
| 0.010 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |